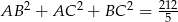/Szkoła średnia/Geometria/Geometria analityczna/Zadania na ekstremum

Zadanie nr 2127264

Dodaj do ulubionych
Dodaj do rozwiązanych

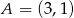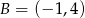Dane są punkty A = (3,1) i B = (− 1,4) oraz prosta 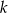k o równaniu 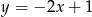y = − 2x+ 1 . Wyznacz taki punkt 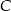C prostej 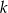k , aby suma kwadratów boków trójkąta 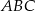ABC była najmniejsza możliwa. Oblicz tę najmniejszą sumę kwadratów długości boków.

Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

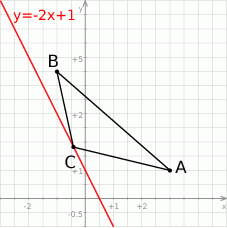
Niech 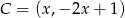C = (x,− 2x + 1) będzie dowolnym punktem prostej 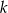k . Ponieważ długość odcinka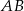 AB

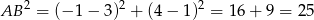
AB 2 = (− 1− 3)2 + (4− 1)2 = 16 + 9 = 25

jest stała, wystarczy sprawdzić, jaka jest najmniejsza możliwa wartość wyrażenia

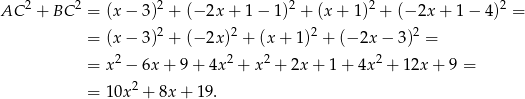
AC 2 + BC 2 = (x − 3)2 + (− 2x + 1 − 1 )2 + (x + 1)2 + (− 2x + 1 − 4)2 = = (x − 3)2 + (− 2x )2 + (x + 1 )2 + (− 2x − 3 )2 = 2 2 2 2 = x − 6x + 9+ 4x + x + 2x + 1 + 4x + 12x + 9 = = 1 0x2 + 8x + 19.

Wykresem otrzymanej funkcji jest parabola o ramionach skierowanych w górę, więc najmniejszą wartość otrzymamy w wierzchołku, czyli dla

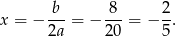
-b- -8- 2- x = − 2a = − 20 = − 5.

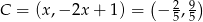Dla tej wartość x mamy ( ) C = (x,− 2x + 1) = − 25, 95 oraz

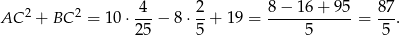
4 2 8 − 16 + 95 87 AC 2 + BC 2 = 10 ⋅---− 8 ⋅--+ 19 = ------------= ---. 25 5 5 5

Cała suma kwadratów długości boków jest więc równa

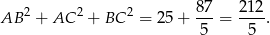
2 2 2 87 212 AB + AC + BC = 25 + -5-= -5--.

 
Odpowiedź: 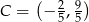( 2 9) C = − 5,5 , 2 2 2 212 AB + AC + BC = 5

Wersja PDF