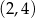/Szkoła średnia/Geometria/Geometria analityczna/Zadania na ekstremum

Zadanie nr 2500049

Dodaj do ulubionych
Dodaj do rozwiązanych

Który z odcinków łączących dowolny punkt paraboli o równaniu 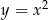2 y = x z punktem 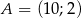A = (10;2) ma najmniejszy kwadrat długości?

Rozwiązanie

Jeżeli oznaczymy dowolny punkt podanej paraboli przez 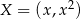2 X = (x,x ) , to kwadrat długości odcinka 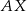AX wyraża się wzorem

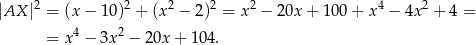
2 2 2 2 2 4 2 |AX | = (x − 10 ) + (x − 2) = x − 2 0x+ 100 + x − 4x + 4 = = x4 − 3x 2 − 20x + 104.

Aby znaleźć wartość najmniejszą tej funkcji liczymy pochodną

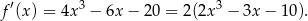
f′(x) = 4x3 − 6x − 2 0 = 2(2x3 − 3x − 1 0).

Łatwo zauważyć, że 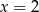x = 2 jest pierwiastkiem tego wielomianu, dzielimy go więc przez x− 2 .

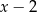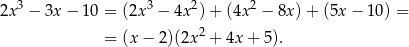
2x3 − 3x − 10 = (2x3 − 4x2) + (4x2 − 8x) + (5x − 10 ) = 2 = (x− 2)(2x + 4x + 5).

Ponieważ trójmian w nawiasie nie ma pierwiastków, 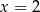x = 2 jest jedynym miejscem zerowym pochodnej, w dodatku w punkcie tym pochodna zmienia znak z ’-’ na ’+’, więc w tym punkcie wyjściowa funkcja osiąga minimum. To minimum jest jednocześnie najmniejszą wartością funkcji.

Na koniec, dla ciekawskich, rysunek sytuacji z treści zadania.

PIC

 
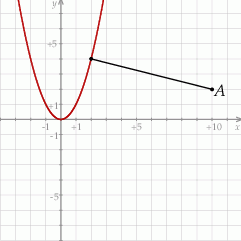
Odpowiedź: (2,4)

Wersja PDF