Zadanie nr 5154135
Na przedziale ![[− 1,7]](https://img.zadania.info/zad/5154135/HzadT0x.gif) określono dwie funkcje:
określono dwie funkcje: 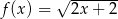 i
i 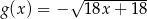 . Rozpatrujemy wszystkie trapezy
. Rozpatrujemy wszystkie trapezy 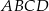 , których wierzchołki
, których wierzchołki 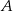 i
i 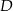 leżą na wykresie funkcji
leżą na wykresie funkcji 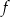 , a wierzchołki
, a wierzchołki 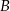 i
i 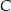 leżą na wykresie funkcji
leżą na wykresie funkcji 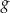 . Podstawy rozpatrywanych trapezów są równoległe do osi
. Podstawy rozpatrywanych trapezów są równoległe do osi 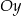 (zobacz rysunek).
(zobacz rysunek).
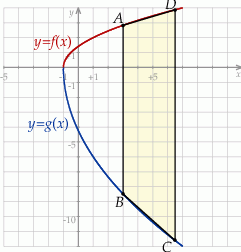
Oblicz współrzędne wierzchołków tego z rozpatrywanych trapezów, w którym 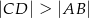 , i który ma największe możliwe pole. Oblicz to największe pole. Przy rozwiązywaniu zadania możesz skorzystać z tego, że jeżeli pierwsza współrzędna wierzchołka
, i który ma największe możliwe pole. Oblicz to największe pole. Przy rozwiązywaniu zadania możesz skorzystać z tego, że jeżeli pierwsza współrzędna wierzchołka 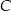 trapezu
trapezu 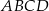 jest równa 7, a druga współrzędna wierzchołka
jest równa 7, a druga współrzędna wierzchołka 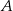 jest równa
jest równa 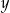 , to pole trapezu wyraża się wzorem
, to pole trapezu wyraża się wzorem
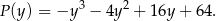
Rozwiązanie
Rozwiązanie tego zadania jest dostępne tylko dla użytkowników z wykupionym abonamentem.
Nie chcesz się rejestrować ani opłacać abonamentu? Zapłać przelewem 7,90 zł lub telefonicznie 9,90 zł, a otrzymasz dwudziestominutowy dostęp do wszystkich materiałów dostępnych w portalu.

