/Szkoła średnia/Geometria/Geometria analityczna/Zadania na ekstremum

Zadanie nr 5569874

Dodaj do ulubionych
Dodaj do rozwiązanych

Znajdź taki punkt 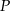P leżący na prostej 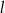l o równaniu 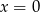x = 0 , z którego odcinek 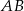AB , gdzie 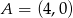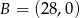A = (4,0) , B = (28,0) , widać pod możliwie największym kątem. Wyznacz ten kąt.

Rozwiązanie

Zastanówmy się najpierw, jak naleźć punkt 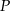P , dla którego kąt 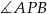∡AP B jest największy możliwy (to jest dokładnie kąt pod jakim widać odcinek 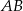AB z punktu P ).

PIC

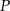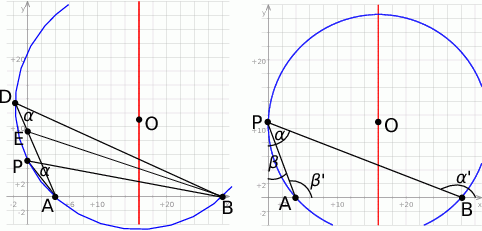
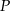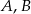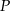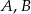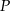Twierdzimy, że P musi być punktem, dla którego okrąg przechodzący przez A ,B i P jest styczny do podanej prostej (tu jest ważne, że punkty leżą po tej samej stronie prostej). Rzeczywiście, gdyby okrąg przechodzący przez A ,B i P przecinał prostą w dwóch punktach, dla dowolnego punktu 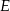E na odcinku łączącym te punkty przecięcia mamy

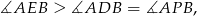
∡AEB > ∡ADB = ∡AP B ,

co oznacza, że 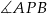∡AP B nie jest maksymalny.

Na początek wyznaczmy środek 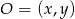O = (x,y ) takiego okręgu. Musi on leżeć na symetralnej odcinka 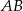AB , czyli na prostej 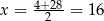x = 4+-28-= 16 2 . Ponadto jego odległość od prostej 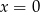x = 0 , czyli 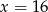x = 16 , musi być równa odległości od punktu 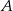A . Mamy więc układ równań.

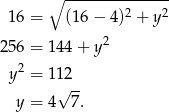
∘ --------------- 16 = (1 6− 4 )2 + y 2 2 2 56 = 144 + y y2 = 112 √ -- y = 4 7.

Zatem 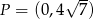√ -- P = (0,4 7) . Prosta 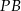P B ma równanie

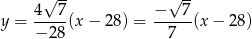
√ -- √ -- 4---7 −---7- y = − 28 (x − 28) = 7 (x − 28)

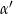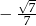Zatem tangens kąta α′ jaki tworzy ta prosta z osią x wynosi √ - − --7 7 . Mamy stąd

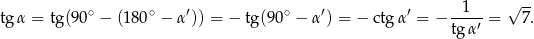
∘ ∘ ′ ∘ ′ ′ --1-- √ -- tg α = tg(90 − (1 80 − α )) = − tg(90 − α ) = − ctg α = − tgα ′ = 7.

Podobnie, ponieważ prosta 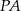PA ma równanie

√ -- √ -- y = 4---7(x − 4) = − 7(x − 4 ), − 4

to mamy

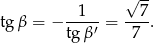
√ -- --1-- --7- tg β = − tg β′ = 7 .

Zatem szukany kąt wynosi

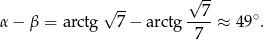
√ -- √ -- 7 ∘ α − β = arctg 7 − arctg ----≈ 49 . 7

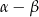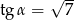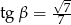Jeżeli ktoś nie lubi funkcji cyklometrycznych to, to można napisać, że szukany kąt wynosi α − β , gdzie √ -- tg α = 7 i √7 tg β = 7-- .  
Odpowiedź: 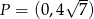√ -- P = (0,4 7) , kąt: √ -- √7- ∘ arctg 7 − arctg 7 ≈ 4 9

Wersja PDF