/Szkoła średnia/Geometria/Geometria analityczna/Zadania na ekstremum

Zadanie nr 6507017

Dodaj do ulubionych
Dodaj do rozwiązanych

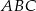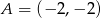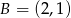Dany jest trójkąt ABC , w którym A = (− 2,− 2) i B = (2 ,1) . Wierzchołek 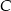C leży na prostej o równaniu 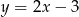y = 2x − 3 . Wyznacz współrzędne wierzchołka 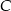C , dla którego suma kwadratów długości boków trójkąta jest najmniejsza.

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

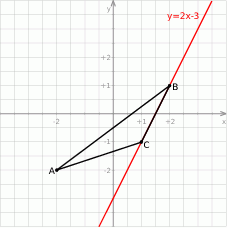
Zauważmy, że wartość 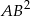AB 2 nie zależy od wyboru punktu 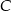C , więc wystarczy wybrać punkt 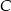C tak, aby suma 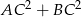AC 2 + BC 2 była najmniejsza. Oznaczmy 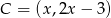C = (x ,2x− 3) . Wtedy

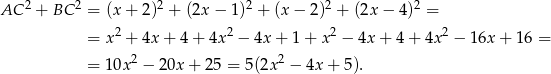
AC 2 + BC 2 = (x + 2)2 + (2x − 1)2 + (x − 2)2 + (2x − 4)2 = 2 2 2 2 = x + 4x + 4 + 4x − 4x+ 1+ x − 4x + 4+ 4x − 16x + 16 = = 10x 2 − 20x + 25 = 5(2x 2 − 4x+ 5).

Wykresem otrzymanej funkcji jest parabola o ramionach skierowanych w górę, więc najmniejszą wartość otrzymamy w wierzchołku, czyli dla 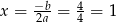−b- 4 x = 2a = 4 = 1 . Wtedy 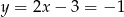y = 2x − 3 = − 1 i C = (1,− 1) .  
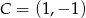Odpowiedź: C = (1,− 1)

Wersja PDF