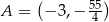Zadanie nr 6603145
Na wykresie funkcji 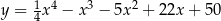 znajdź współrzędne punktu
znajdź współrzędne punktu 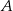 , którego odległość od prostej o równaniu
, którego odległość od prostej o równaniu 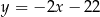 jest najmniejsza.
jest najmniejsza.
Rozwiązanie
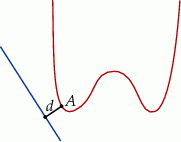
Ze względu na skomplikowany wzór danego wielomianu trudno oczywiście zrobić dokładny rysunek, więc rysujemy schematycznie o co może chodzić w zadaniu. Niech
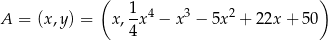
będzie szukanym punktem.
Korzystamy ze wzoru na odległość punktu 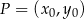 od prostej
od prostej 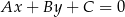 :
:
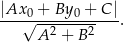
Odległość punktu 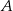 od podanej prostej
od podanej prostej 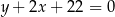 jest więc
jest więc
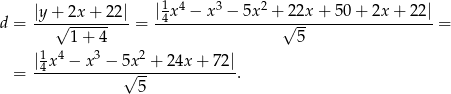
równa
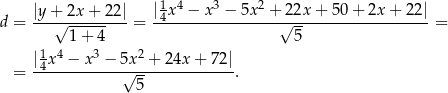
Aby ustalić jaka jest najmniejsza możliwa wartość tego wyrażenia musimy zbadać funkcję, która znajduje się pod wartością bezwzględną.
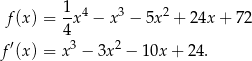
Aby rozłożyć otrzymany wielomian stopnia 3 szukamy jego pierwiastków całkowitych. Sprawdzając dzielniki wyrazu wolnego można znaleźć pierwiastek 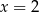 . Dzielimy teraz
. Dzielimy teraz 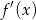 przez
przez 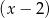 , my zrobimy to grupując wyrazy.
, my zrobimy to grupując wyrazy.
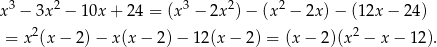
Rozkładamy jeszcze trójmian w nawiasie.
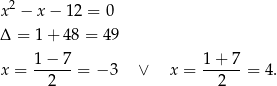
Pochodna jest więc równa
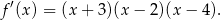
Widzimy teraz, że pochodna jest dodatnia w przedziałach 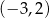 i
i 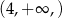 , oraz ujemna w przedziałach
, oraz ujemna w przedziałach 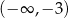 i
i 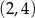 .
.
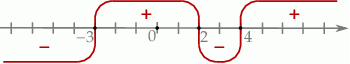
To oznacza, że funkcja 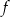 rośnie w pierwszych dwóch przedziałach i maleje w dwóch kolejnych. W szczególności w punktach
rośnie w pierwszych dwóch przedziałach i maleje w dwóch kolejnych. W szczególności w punktach 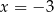 i
i 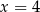 funkcja
funkcja 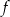 ma minima lokalne i w jednym z tych punktów przyjmuje najmniejszą swoją wartość. Aby ustalić w którym, liczymy
ma minima lokalne i w jednym z tych punktów przyjmuje najmniejszą swoją wartość. Aby ustalić w którym, liczymy 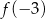 i
i 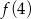 .
.
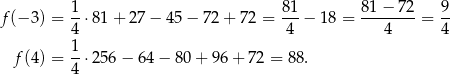
Widzimy zatem, że funkcja 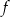 przyjmuje wyłącznie wartości dodatnie i jej najmniejszą wartość otrzymujemy dla
przyjmuje wyłącznie wartości dodatnie i jej najmniejszą wartość otrzymujemy dla 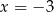 . To oznacza, że interesująca nas odległość punktu
. To oznacza, że interesująca nas odległość punktu 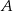 od danej prostej
od danej prostej
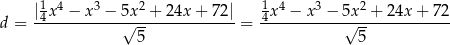
jest najmniejsza, gdy pierwsza współrzędna punktu 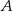 jest równa
jest równa 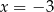 . Obliczamy jeszcze drugą współrzędną punktu
. Obliczamy jeszcze drugą współrzędną punktu 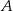 .
.
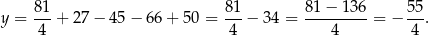
Zatem 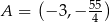 .
.
Na koniec (dla ciekawskich) dokładny rysunek całej sytuacji – z daleka i w powiększeniu.
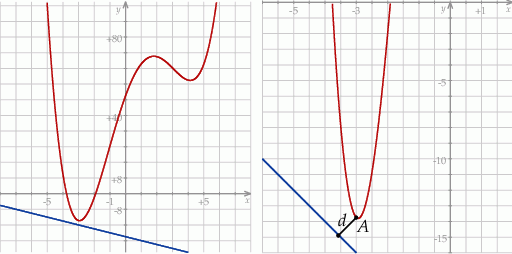
Odpowiedź: