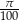Zadanie nr 7857580
Wyznacz wartość parametru 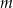 , dla której pole koła stycznego do prostych zawierających boki
, dla której pole koła stycznego do prostych zawierających boki 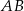 i
i 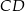 równoległoboku
równoległoboku 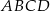 o wierzchołkach
o wierzchołkach 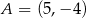 ,
, 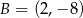 ,
, 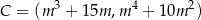 jest najmniejsze możliwe. Oblicz to pole.
jest najmniejsze możliwe. Oblicz to pole.
Rozwiązanie
Szkicujemy równoległobok.
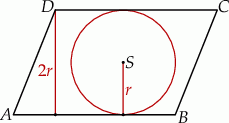
Promień okręgu stycznego do prostych 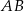 i
i 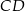 to dokładnie połowa odległości między tymi prostymi, czyli połowa odległości punktu
to dokładnie połowa odległości między tymi prostymi, czyli połowa odległości punktu 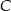 od prostej
od prostej 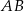 . Aby obliczyć tę odległość piszemy najpierw równanie prostej
. Aby obliczyć tę odległość piszemy najpierw równanie prostej 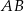 . Szukamy prostej w postaci
. Szukamy prostej w postaci 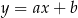 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów 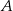 i
i 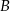 .
.
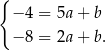
Odejmujemy od pierwszego równania drugie i mamy.
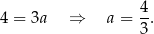
Stąd
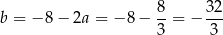
i prosta 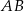 ma równanie
ma równanie
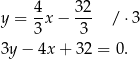
Korzystamy teraz ze wzoru na odległość punktu 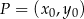 od prostej
od prostej 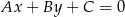 :
:
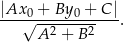
Odległość punktu 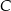 od prostej
od prostej 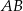 jest więc równa
jest więc równa
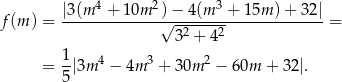
Sprawdzamy teraz jakie wartości może przyjmować wielomian pod wartością bezwzględną.
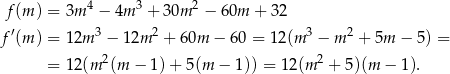
Ponieważ pochodna ma tylko jedno miejsce zerowe i zmienia w nim znak z ujemnego na dodatni, funkcja 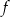 maleje na przedziale
maleje na przedziale 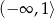 i rośnie na przedziale
i rośnie na przedziale 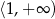 . Najmniejszą wartością tej funkcji jest więc
. Najmniejszą wartością tej funkcji jest więc
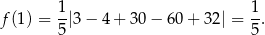
Promień koła stycznego do boków  i
i  jest więc równy
jest więc równy
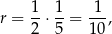
a jego pole to
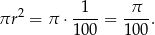
Odpowiedź: 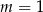 ,
,