Zadanie nr 8457009
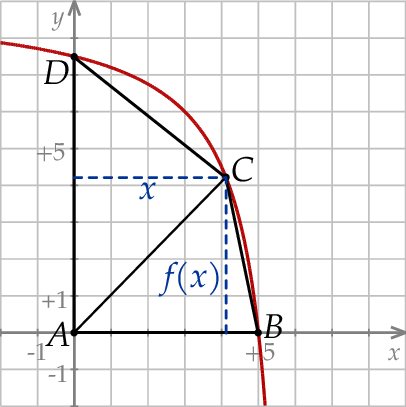
Na rysunku poniżej przedstawiono fragment wykresu funkcji 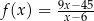 określonej dla
określonej dla 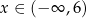 . Wykres ten przecina osie
. Wykres ten przecina osie 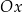 i
i 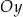 odpowiednio w punktach
odpowiednio w punktach 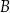 i
i 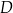 , a punkt
, a punkt 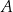 jest początkiem układu współrzędnych. Rozpatrujemy wszystkie czworokąty
jest początkiem układu współrzędnych. Rozpatrujemy wszystkie czworokąty 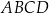 , w których punkt
, w których punkt 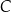 leży na wykresie funkcji
leży na wykresie funkcji 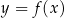 pomiędzy punktami
pomiędzy punktami 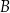 i
i 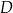 .
.
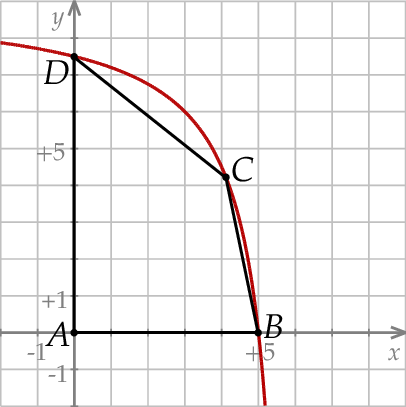
Oblicz współrzędne wierzchołka 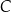 tego z rozpatrywanych czworokątów, którego pole jest największe.
tego z rozpatrywanych czworokątów, którego pole jest największe.
Rozwiązanie
Wyznaczmy najpierw współrzędne punktów 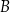 i
i 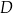 .
.
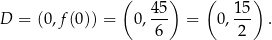
Aby wyznaczyć współrzędne punktu 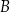 rozwiązujemy równanie
rozwiązujemy równanie

Zatem 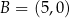 .
.
Aby obliczyć pole czworokąta  dzielimy go na 2 trójkąty przekątną
dzielimy go na 2 trójkąty przekątną  .
.
Jeżeli 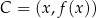 , to interesujące nas pole jest równe
, to interesujące nas pole jest równe
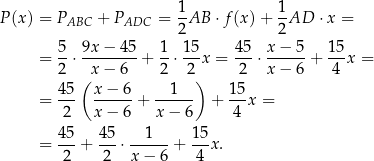
Liczymy pochodną tej funkcji.
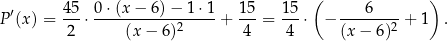
Sprawdzamy teraz kiedy pochodna jest równa 0.
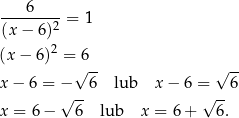
Drugie rozwiązanie nie należy do dziedziny 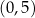 interesującej nas funkcji. Zauważmy jeszcze, że funkcja
interesującej nas funkcji. Zauważmy jeszcze, że funkcja 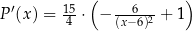 jest malejąca w przedziale
jest malejąca w przedziale 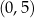 (bo
(bo 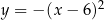 jest rosnąca na tym przedziale), więc pochodna w punkcie
jest rosnąca na tym przedziale), więc pochodna w punkcie 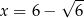 zmienia znak z dodatniego na ujemny. To oznacza, że w tym punkcie funkcja
zmienia znak z dodatniego na ujemny. To oznacza, że w tym punkcie funkcja 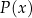 ma maksimum i jest to wartość pierwszej współrzędnej szukanego wierzchołka
ma maksimum i jest to wartość pierwszej współrzędnej szukanego wierzchołka 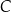 , dla której pole czworokąta
, dla której pole czworokąta 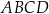 jest największe. Obliczmy jeszcze drugą współrzędną
jest największe. Obliczmy jeszcze drugą współrzędną
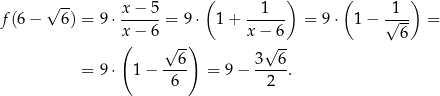
Odpowiedź: