/Szkoła średnia/Prawdopodobieństwo/Niezależność

Zadanie nr 2806766

Dodaj do ulubionych
Dodaj do rozwiązanych

W sekretariacie stoją dwa telefony - biały i czarny. Telefony te dzwonią niezależnie od siebie. Prawdopodobieństwo, że w ciągu najbliższych pięciu minut zadzwoni telefon biały, jest równe 0,5. Prawdopodobieństwo, że w ciągu najbliższych pięciu minut zadzwoni telefon czarny, jest równe 0,4. Oblicz prawdopodobieństwo, że w ciągu najbliższych pięciu minut zadzwoni co najmniej jeden z telefonów.

Rozwiązanie

Sposób I

Oznaczmy przez

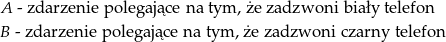
A -zdarzenie polegające na tym, że zadzwoni bia ły telefon B -zdarzenie polegaj ące na tym, że zadzwoni czarny telefon

Zatem 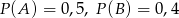P(A ) = 0,5 , P (B) = 0,4 i mamy obliczyć 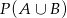P (A ∪ B ) . Wiemy ponadto, że telefony dzwonią niezależnie od siebie, więc

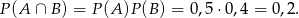
P (A ∩ B ) = P(A )P (B) = 0 ,5 ⋅0,4 = 0,2.

Zatem

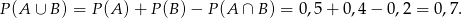
P (A ∪ B ) = P(A ) + P(B )− P(A ∩ B) = 0,5 + 0,4 − 0,2 = 0,7.

Sposób II

Oznaczmy przez

A - zdarzenie polegaj ące na tym, że zadzwoni co najmniej jeden telefon B -zdarzenie polegające na tym, że nie zadzwoni żaden telefon

Łatwiej jest policzyć jest prawdopodobieństwo zdarzenia 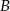B . Prawdopodobieństwo, że w ciągu najbliższych pięciu minut nie zadzwoni telefon biały jest równe 0,5. Natomiast prawdopodobieństwo, że nie zadzwoni czarny wynosi 0,6. Zatem prawdopodobieństwo, że nie zadzwoni żaden jest równe

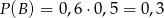
P(B ) = 0,6⋅ 0,5 = 0,3

(bo telefony dzwonią niezależnie). Stąd

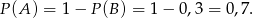
P(A ) = 1 − P (B ) = 1 − 0,3 = 0,7.

 
Odpowiedź: 0,7

Wersja PDF