/Szkoła średnia/Prawdopodobieństwo/Niezależność

Zadanie nr 3174402

W procesie produkcyjnym na stanowisku 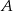A powstaje 2% braków, na stanowisku 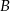B 5% braków. Z każdego stanowiska pobrano po jednej sztuce wyrobu. Obliczyć prawdopodobieństwo, że

  • obydwie sztuki są dobre;
  • tylko jedna sztuka jest dobra.
Wersja PDF

Rozwiązanie

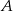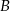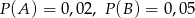Opisane zdarzenia, czyli pobranie przedmiotu z każdego ze stanowisk są oczywiście niezależne. Niech A i B będą zdarzeniami, że przedmiot pobrany odpowiednio ze stanowiska I i II jest brakiem. Mamy więc P (A ) = 0,02, P(B ) = 0,05 .

  • Szukamy 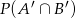′ ′ P(A ∩ B ) . Z niezależności mamy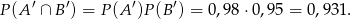
    ′ ′ ′ ′ P(A ∩ B ) = P (A )P (B ) = 0,98 ⋅0,95 = 0,931.

     
    Odpowiedź: 0,931

  • Mamy policzyć 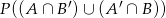′ ′ P((A ∩ B )∪ (A ∩ B )) . Ponieważ zdarzenia te są rozłączne, mamy (z niezależności)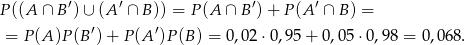
    P((A ∩ B′)∪ (A ′ ∩ B )) = P(A ∩ B′)+ P(A ′ ∩ B) = ′ ′ = P(A )P (B )+ P(A )P (B) = 0,02⋅ 0,95+ 0,05 ⋅0,98 = 0,0 68.

     
    Odpowiedź: 0,068

Wersja PDF