/Szkoła średnia/Prawdopodobieństwo/Niezależność

Zadanie nr 6404483

Rzucamy dwa razy kostką do gry. Niech 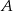A oznacza zdarzenie suma wyrzuconych oczek jest większa od 7, a 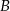B zdarzenie, że iloczyn wyrzuconych oczek jest mniejszy od 48.

  • Oblicz 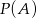P(A ) i P (B) .
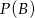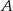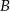  • Sprawdź czy zdarzenia A i B są niezależne,
  • Oblicz 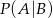P(A |B) i P (B|A ) .
Wersja PDF

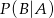Rozwiązanie

  • Iloczyn oczek jest zawsze mniejszy od 48, więc 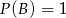P(B ) = 1 . Wypiszmy zdarzenia sprzyjające do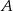 A
    (2,6 ), (3,5 ),(3,6), (4,4 ),(4,5),(4,6) (5,3 ),(5,4),(5,5),(5,6) (6,2 ),(6,3),(6,4),(6,5),(6,6).

    Wszystkich zdarzeń jest 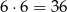6 ⋅6 = 36 , więc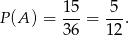

    P(A ) = 1-5 = -5-. 3 6 12

     
    Odpowiedź: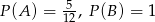 P(A ) = 5-, P (B) = 1 12

  • Sprawdźmy
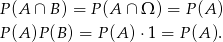
    P (A ∩ B ) = P(A ∩ Ω) = P(A ) P (A)P (B) = P(A )⋅ 1 = P(A ).

    Zdarzenia są więc niezależne.  
    Odpowiedź: Tak, są niezależne.

  • Liczymy
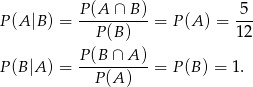
    P (A|B ) = P-(A-∩-B)-= P(A ) = -5- P (B) 1 2 P (B ∩ A) P (B|A ) = ----------= P(B ) = 1. P (A)

     
    Odpowiedź: 5- P(A |B ) = 12, P (B|A ) = 1

Wersja PDF