/Szkoła średnia/Prawdopodobieństwo/Niezależność

Zadanie nr 8363947

W urnie jest 6 kul białych i 4 czarne. Wyjęto losowo 2 kule i określono zdarzenia: 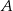A – wylosowanie co najwyżej 1 kuli białej, 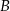B – wylosowanie co najwyżej jednej kuli czarnej. Sprawdź, czy te zdarzenia są niezależne.

Wersja PDF

Rozwiązanie

Musimy sprawdzić czy

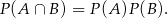
P (A ∩ B ) = P(A )P (B).

Aby to zrobić, obliczymy te prawdopodobieństwa. Jeżeli za zdarzenia elementarne traktujemy pary nieuporządkowane wylosowanych kul, to

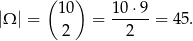
( ) 10 10-⋅9- |Ω | = 2 = 2 = 45.

Obliczmy, ile jest zdarzeń sprzyjających do 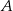A . Są one dwóch typów: wylosowano same kule czarne, takich zdarzeń jest 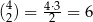4 4⋅3- (2) = 2 = 6 , lub wylosowano jedną białą i jedną czarną, takich zdarzeń jest 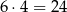6⋅4 = 24 . Mamy zatem

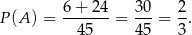
P(A ) = 6-+-2-4 = 30-= 2-. 4 5 45 3

Podobnie liczymy prawdopodobieństwo zdarzenia 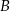B .

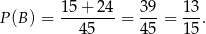
P(B ) = 15-+-24-= 39-= 13-. 45 45 15

Zdarzenie 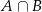A ∩ B , to wylosowanie jednej kuli białej i jednej czarnej, czyli

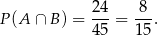
24- 8-- P (A ∩ B) = 45 = 15.

Widać, że 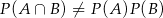P (A ∩ B ) ⁄= P(A )P (B) .  
Odpowiedź: Nie są niezależne.

Wersja PDF