/Szkoła średnia/Funkcje/Wielomiany/Dzielenie z resztą/Przez stopnia 3

Zadanie nr 7997712

Wykaż, że jeżeli wielomian 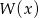W (x) jest podzielny przez 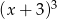3 (x + 3 ) , to wielomian 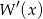W ′(x) jest podzielny przez (x + 3)2 .

Wersja PDF

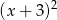Rozwiązanie

Jeżeli 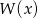W (x) jest podzielny przez

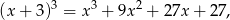
3 3 2 (x + 3) = x + 9x + 27x + 27,

to

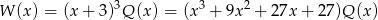
3 3 2 W (x ) = (x+ 3) Q (x) = (x + 9x + 27x + 27)Q (x)

dla pewnego wielomianu 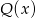Q (x) . Liczymy teraz pochodną – korzystamy ze wzoru na pochodną iloczynu.

[ ] W ′(x) = (x + 3)3 ′Q (x) + (x + 3)3Q ′(x) = [ 3 2 ]′ 3 ′ = x + 9x + 27x + 27 Q (x) + (x + 3) Q (x ) = ( 2 ) 3 ′ = 3x + 18x + 27 Q (x)+ (x + 3) Q (x ) = 2 3 ′ = 3(x + 3) Q (x) + (x + 3) Q (x) = = (x + 3)2[3Q (x )+ (x + 3)Q ′(x)] .

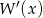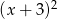Widać teraz, że rzeczywiście ′ W (x) dzieli się przez 2 (x + 3) .

Wersja PDF