Zadanie nr 2772796
Dla jakich wartości parametru 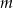 wielomian
wielomian 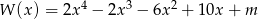 ma pierwiastek trzykrotny?
ma pierwiastek trzykrotny?
Rozwiązanie
Sposób I
Najprostsze rozwiązanie otrzymamy używając pochodnej. Łatwo uzasadnić, że 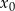 jest pierwiastkiem
jest pierwiastkiem 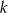 –krotnym wielomianu wtedy i tylko wtedy gdy jest pierwiastkiem
–krotnym wielomianu wtedy i tylko wtedy gdy jest pierwiastkiem 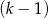 – krotnym jego pochodnej. W naszej sytuacji chcemy aby
– krotnym jego pochodnej. W naszej sytuacji chcemy aby 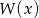 ,
, 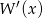 i
i 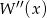 miały wspólny pierwiastek. Liczymy
miały wspólny pierwiastek. Liczymy
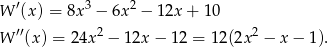
Zobaczmy jakie pierwiastki ma otrzymany trójmian kwadratowy.
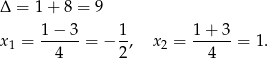
Łatwo sprawdzić, że 1 jest pierwiastkiem 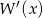 , a
, a 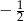 nie jest. Zatem potencjalnym pierwiastkiem trzykrotnym wyjściowego wielomianu jest
nie jest. Zatem potencjalnym pierwiastkiem trzykrotnym wyjściowego wielomianu jest 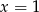 . Ponieważ wiemy już, że jest to pierwiastek
. Ponieważ wiemy już, że jest to pierwiastek 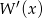 i
i 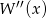 wystarczy sprawdzić kiedy jest to pierwiastek
wystarczy sprawdzić kiedy jest to pierwiastek 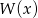 .
.
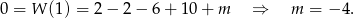
Sposób II
Jeżeli wielomian ma mieć pierwiastek 3–krotny, to musimy mieć równość
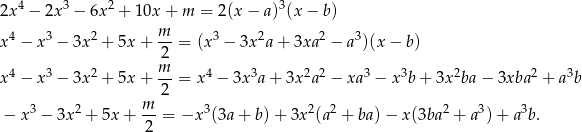
Daje to nam układ równań
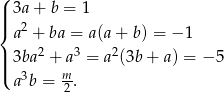
Z pierwszego równania wyliczamy 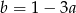 i wstawiamy do drugiego
i wstawiamy do drugiego
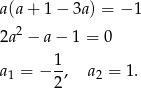
Łatwo sprawdzić, że 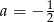 i
i 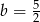 prowadzi do sprzeczności w 3 równaniu. Zatem
prowadzi do sprzeczności w 3 równaniu. Zatem 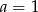 i
i 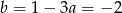 . Stąd
. Stąd
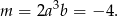
Sposób III
Korzystamy ze wzorów Viète’a dla równania 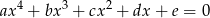 .
.
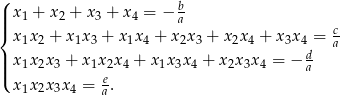
W naszej sytuacji równanie ma mieć pierwiastek 3–krotny  i jeszcze jeden pierwiastek
i jeszcze jeden pierwiastek 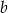 , zatem
, zatem
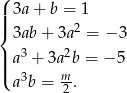
No i mamy ten sam układ równań co w poprzednim sposobie.
Odpowiedź: