/Szkoła średnia/Równania/Wielomianowe/Stopnia 4/Z parametrem

Zadanie nr 3650840

Dodaj do ulubionych
Dodaj do rozwiązanych

Dla jakich wartości parametru 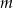m równanie 2 2 (x − m ) [m(x − m ) − m − 1]+ 1 = 0 ma więcej pierwiastków dodatnich niż ujemnych?

Rozwiązanie

Równanie aż się prosi, żeby podstawić 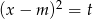2 (x − m ) = t .

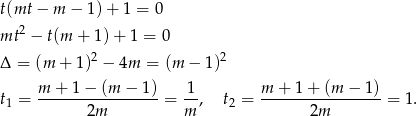
t(mt − m − 1) + 1 = 0 mt 2 − t(m + 1) + 1 = 0 2 2 Δ = (m + 1) − 4m = (m − 1 ) m + 1 − (m − 1) 1 m + 1+ (m − 1) t1 = -----------------= --, t2 = -----------------= 1. 2m m 2m

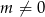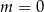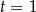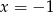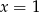W powyższych przekształceniach zaczęliśmy zakładać, że m ⁄= 0 , zauważmy, że dla m = 0 mamy równanie t = 1 , które daje x = − 1 i x = 1 , a więc żadany w treści warunek nie jest spełniony.

Rozważmy teraz kilka możliwych sytuacji.

Jeżeli 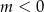m < 0 , to równanie 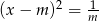(x− m )2 = 1- m nie ma rozwiązań i pozostaje nam

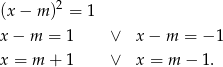
(x− m )2 = 1 x− m = 1 ∨ x − m = − 1 x = m + 1 ∨ x = m − 1.

Co najmniej jeden z tych pierwiatków jest ujemny (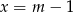x = m − 1 ), więc na pewno żądany warunek nie zachodzi.

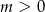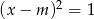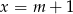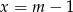Jeżeli m > 0 to równość 2 (x− m) = 1 daje nam tak jak poprzednio x = m + 1 lub x = m − 1 , ale mamy jeszcze

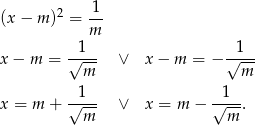
1 (x − m)2 = -- m x − m = √1-- ∨ x − m = − √-1- m m 1 1 x = m + √--- ∨ x = m − √---. m m

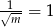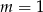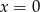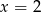Ponadto wśród czterech otrzymanych pierwiastków mogą być dwa równe tylko dla √1m--= 1 , czyli dla m = 1 . Wtedy mamy dwa pierwiastki x = 0 i x = 2 , a więc żadany warunek zachodzi.

Jeżeli 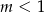m < 1 to z tych czterech liczb tylko dwie są dodatnie. Jeżeli natomiast 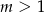m > 1 to wszystkie są dodatnie.  
Odpowiedź: m ≥ 1

Wersja PDF