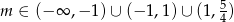Zadanie nr 4047984
Wyznacz wszystkie wartości parametru 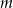 , dla których wielomian
, dla których wielomian
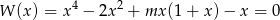
ma 4 różne pierwiastki.
Rozwiązanie
Jeden pierwiastek widać gołym okiem: 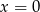 . Możemy więc podzielić dany wielomian przez
. Możemy więc podzielić dany wielomian przez  i pamiętać, że w dalszej części mają nam wychodzić niezerowe pierwiastki. Pozostaje nam równanie
i pamiętać, że w dalszej części mają nam wychodzić niezerowe pierwiastki. Pozostaje nam równanie
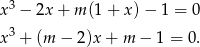
Nie bardzo widać co dalej, więc spróbujmy poszukać jakiegoś pierwiastka tego równania. Trochę kombinując można znaleźć: 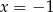 . W takim razie dzielimy wielomian przez
. W takim razie dzielimy wielomian przez 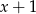 (my jak zwykle grupujemy wyrazy).
(my jak zwykle grupujemy wyrazy).
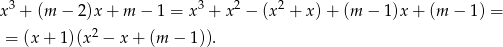
Teraz sprawdzamy, kiedy otrzymane równanie kwadratowe ma dwa różne pierwiastki.
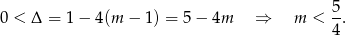
To jeszcze nie koniec, bo musimy sprawdzić, czy przypadkiem 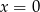 lub
lub 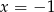 nie jest pierwiastkiem tego trójmianu (bo mają być cztery różne pierwiastki). Sprawdzamy kiedy tak jest (wstawiamy
nie jest pierwiastkiem tego trójmianu (bo mają być cztery różne pierwiastki). Sprawdzamy kiedy tak jest (wstawiamy 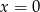 i
i 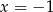 ) do trójmianu.
) do trójmianu.
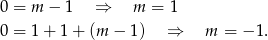
Musimy te dwie wartości 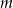 wyrzucić ze zbioru rozwiązań.
wyrzucić ze zbioru rozwiązań.
Odpowiedź: