/Szkoła średnia/Równania/Wielomianowe/Stopnia 4/Z parametrem

Zadanie nr 4395756

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz te wartości parametru 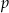p , dla których równanie 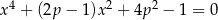x 4 + (2p − 1)x2 + 4p2 − 1 = 0 ma dokładnie dwa różne pierwiastki rzeczywiste.

Rozwiązanie

Podstawiamy 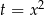2 t = x i mamy równanie kwadratowe

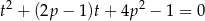
2 2 t + (2p − 1)t+ 4p − 1 = 0

Aby wyjściowe równanie miało dokładnie dwa pierwiastki, powyższe równanie kwadratowe musi mieć dokładnie jeden pierwiastek dodatni (da on nam dwa x –y). Sprawdźmy kiedy równanie ma pierwiastki.

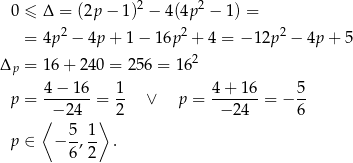
0 ≤ Δ = (2p − 1 )2 − 4(4p 2 − 1) = 2 2 2 = 4p − 4p + 1 − 16p + 4 = − 12p − 4p + 5 Δ = 16+ 240 = 256 = 162 p p = 4−--16-= 1- ∨ p = 4+--16-= − 5- − 24 2 − 24 6 ⟨ 5 1⟩ p ∈ − --,-- . 6 2

Sprawdźmy teraz kiedy dokładnie jeden z pierwiastków jest dodatni.

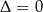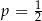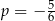Na początek sprawdźmy sytuacje gdy Δ = 0 , czyli p = 12 lub p = − 56 . Mamy wtedy równania

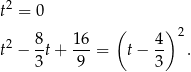
t2 = 0 ( ) 2 t2 − 8t+ 16-= t − 4- . 3 9 3

Widać więc, że w drugiej sytuacji otrzymujemy równanie z jednym pierwiastkiem dodatnim, więc będą spełnione warunki zadania.

Jeżeli 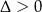Δ > 0 , to pytamy się, kiedy pierwiastki są różnych znaków (żeby dostać 2, a nie 4 wartości x ). Na mocy wzorów Viète’a tak będzie, gdy

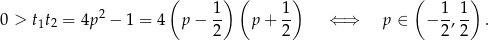
( 1) ( 1) ( 1 1) 0 > t1t2 = 4p 2 − 1 = 4 p − -- p + -- ⇐ ⇒ p ∈ − -, -- . 2 2 2 2

Łącząc otrzymane rozwiązania, otrzymujemy więc

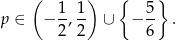
( ) { } 1-1- 5- p ∈ − 2,2 ∪ − 6 .

 
Odpowiedź: ( 1 1) { 5} p ∈ − 2,2 ∪ − 6

Wersja PDF