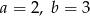/Szkoła średnia/Równania/Wielomianowe/Stopnia 4/Z parametrem

Zadanie nr 5193224

Dodaj do ulubionych
Dodaj do rozwiązanych

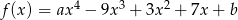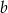Wielomian f jest określony wzorem 4 3 2 f (x) = ax − 9x + 3x + 7x + b dla pewnych liczb pierwszych a oraz b . Wiadomo, ze liczba 32 jest pierwiastkiem tego wielomianu. Oblicz a i b .

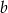Rozwiązanie

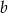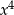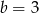W rozwiązaniu będziemy korzystać z twierdzenia o wymiernych pierwiastkach wielomianów. Na mocy tego twierdzenia liczba 3 musi dzielić wyraz wolny, czyli b , a liczba 2 musi dzielić współczynnik przy x4 , czyli a . Jednak jedyna liczba pierwsza podzielna przez 3 to 3, czyli b = 3 . Podobnie, jedyna parzysta liczba pierwsza to 2, czyli a = 2 .

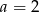Na koniec możemy (ale nie musimy) sprawdzić, że liczba 3 2 rzeczywiście jest pierwiastkiem wielomianu

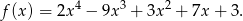
f (x) = 2x 4 − 9x 3 + 3x 2 + 7x+ 3.

Liczymy

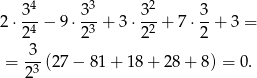
3-4 3-3 32- 3- 2 ⋅2 4 − 9 ⋅2 3 + 3⋅ 22 + 7⋅ 2 + 3 = 3 = -3-(2 7− 81+ 18+ 28+ 8) = 0. 2

 
Odpowiedź: a = 2 , b = 3

Wersja PDF