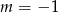Zadanie nr 5594855
Wyznacz wszystkie wartości parametru 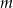 , dla których równanie
, dla których równanie
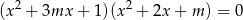
ma cztery różne pierwiastki, których suma sześcianów jest równa 4.
Rozwiązanie
Pierwiastki podanego równania to pierwiastki pierwszego i drugiego równania kwadratowego. Powiedzmy, że pierwiastki pierwszego to 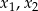 , a pierwiastki drugiego to
, a pierwiastki drugiego to 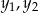 . Na mocy wzorów Viète’a mamy zatem
. Na mocy wzorów Viète’a mamy zatem
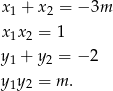
Na razie nie przejmujmy się  -ami, ani tym, czy przypadkiem, któreś z tych pierwiastków są równe – sprawdzimy to na samym końcu.
-ami, ani tym, czy przypadkiem, któreś z tych pierwiastków są równe – sprawdzimy to na samym końcu.
Liczymy teraz sumę sześcianów pierwiastków
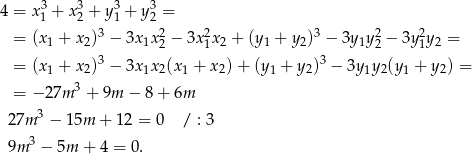
Szukamy teraz pierwiastków wymiernych otrzymanego równania. Łatwo zauważyć, że pierwiastkiem jest 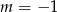 , czyli równanie dzieli się przez
, czyli równanie dzieli się przez 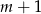 . My dzielimy grupując wyrazy.
. My dzielimy grupując wyrazy.
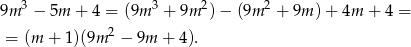
Trójmian w nawiasie nie ma pierwiastków, więc jedyna możliwość to 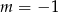 . Mamy wtedy równanie
. Mamy wtedy równanie
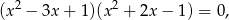
które jak łatwo sprawdzić ma cztery różne pierwiastki
Odpowiedź: