/Szkoła średnia/Równania/Wielomianowe/Stopnia 4/Z parametrem

Zadanie nr 6136024

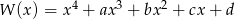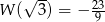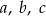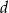Pierwiastki wielomianu 4 3 2 W (x) = x + ax + bx + cx+ d tworzą czterowyrazowy ciąg arytmetyczny o sumie wyrazów równej zero. Wiadomo ponadto, że √ -- W ( 3) = − 23 9 . Oblicz współczynniki a, b, c i d . Rozważ wszystkie możliwe przypadki.

Wersja PDF

Rozwiązanie

Jeżeli pierwiastki wielomianu są kolejnymi wyrazami ciągu arytmetycznego, to możemy je oznaczyć jako: 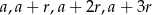a,a + r,a + 2r,a + 3r . Wiemy ponadto, że suma wyrazów tego ciągu jest równa zero, więc

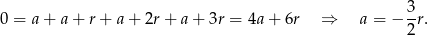
0 = a + a + r+ a+ 2r+ a + 3r = 4a+ 6r ⇒ a = − 3-r. 2

Pierwiastki wielomianu są więc równe

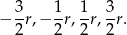
3- 1- 1- 3- − 2 r,− 2r,2 r,2r.

To oznacza, że wielomian 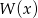W (x ) ma postać

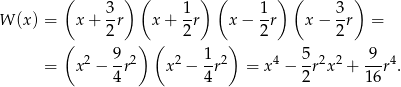
( ) ( ) ( ) ( ) 3 1 1 3 W (x) = x + 2-r x + 2r x − 2r x − 2r = ( ) ( ) 2 9-2 2 1-2 4 5-2 2 -9- 4 = x − 4 r x − 4r = x − 2r x + 1 6r .

Pozostało teraz skorzystać z podanego warunku 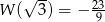√ -- W ( 3) = − 23 9 .

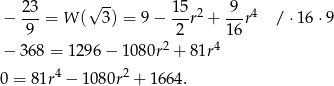
23 √ -- 15 9 − ---= W ( 3) = 9 − --r2 + ---r4 / ⋅16 ⋅9 9 2 16 − 368 = 1296 − 1080r2 + 81r4 4 2 0 = 8 1r − 1 080r + 1664.

Podstawiamy 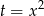2 t = x i mamy

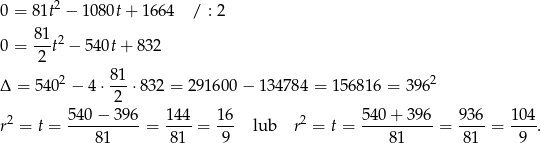
2 0 = 81t − 108 0t+ 1 664 / : 2 81-2 0 = 2 t − 540t+ 832 81 Δ = 5402 − 4 ⋅---⋅832 = 291600 − 13 4784 = 15 6816 = 3 962 2 r2 = t = 54-0−--396 = 144-= 16- lub r2 = t = 54-0+--396 = 936-= 104. 81 81 9 81 81 9

Są zatem dwa wielomiany spełniające warunki zadania:

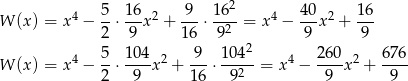
5 16 9 16 2 40 16 W (x ) = x4 − --⋅---x2 + ---⋅--2-= x4 − ---x2 + --- 2 9 16 9 2 9 9 4 5- 104- 2 -9- 1-04- 4 2-60 2 67-6 W (x ) = x − 2 ⋅ 9 x + 16 ⋅ 92 = x − 9 x + 9

 
Odpowiedź: { ( 40 16 ) ( 260 676 )} (a,b,c,d) ∈ 0,− -9 ,0, 9 , 0 ,− 9-,0 ,-9-

Wersja PDF