/Szkoła średnia/Równania/Wielomianowe/Stopnia 4/Z parametrem

Zadanie nr 8914961

Zbadaj, dla jakich wartości parametru 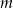m równanie 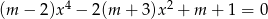4 2 (m − 2)x − 2(m + 3)x + m + 1 = 0 ma cztery różne pierwiastki rzeczywiste.

Wersja PDF

Rozwiązanie

Podstawiając 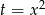2 t = x mamy równanie

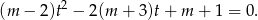
2 (m − 2)t − 2(m + 3)t + m + 1 = 0.

Aby wyjściowe równanie miało cztery pierwiastki, powyższe równanie musi być kwadratowe (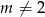m ⁄= 2 ) oraz musi mieć dwa pierwiastki dodatnie (każdy z nich da dwa x -y).

Sprawdźmy na początek kiedy równanie ma dwa pierwiastki.

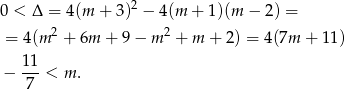
0 < Δ = 4 (m + 3)2 − 4(m + 1)(m − 2) = = 4 (m2 + 6m + 9 − m 2 + m + 2) = 4 (7m + 11 ) 11 − ---< m . 7

Na mocy wzorów Viète’a pierwiastki będą dodatnie gdy

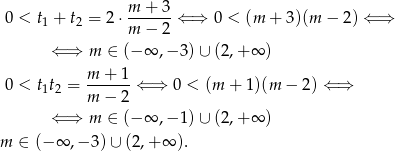
m + 3 0 < t1 + t2 = 2 ⋅m-−--2 ⇐ ⇒ 0 < (m + 3)(m − 2 ) ⇐ ⇒ ⇐ ⇒ m ∈ (− ∞ ,− 3) ∪ (2,+ ∞ ) m + 1 0 < t1t2 = ------⇐ ⇒ 0 < (m + 1)(m − 2) ⇐ ⇒ m − 2 ⇐ ⇒ m ∈ (− ∞ ,− 1) ∪ (2,+ ∞ ) m ∈ (− ∞ ,− 3) ∪ (2,+ ∞ ).

W połączeniu z warunkiem na 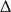Δ -ę mamy m ∈ (2,+ ∞ ) .  
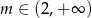Odpowiedź: m ∈ (2+ ∞ )

Wersja PDF