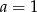Zadanie nr 9989269
Liczby 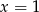 i
i 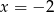 są pierwiastkami wielomianu
są pierwiastkami wielomianu 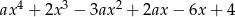 . Wiedząc, że wielomian ten jest kwadratem wielomianu stopnia 2, oblicz
. Wiedząc, że wielomian ten jest kwadratem wielomianu stopnia 2, oblicz  .
.
Rozwiązanie
Na początku należy się zastanowić, jaką informację niesie fakt, że wielomian jest kwadratem innego wielomianu? Odpowiedź jest podobna jak dla liczb, jeżeli wielomian przez coś się dzieli to od razu dzieli się również przez kwadrat tego czegoś. W szczególności każdy z pierwiastków tego wielomianu musi być jego pierwiastkiem podwójnym.
Sposób I
Skoro 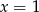 jest pierwiastkiem, to dzielimy przez
jest pierwiastkiem, to dzielimy przez 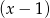 . Robimy to jak kto umie, schemat Hornera, dzielenie wielomianów lub grupowanie odpowiednich czynników. My zrobimy to tą ostatnią metodą.
. Robimy to jak kto umie, schemat Hornera, dzielenie wielomianów lub grupowanie odpowiednich czynników. My zrobimy to tą ostatnią metodą.
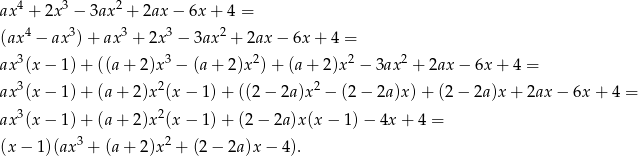
Jak już zauważyliśmy, 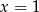 ma być również pierwiastkiem otrzymanego wielomianu stopnia 3. Łatwo sprawdzić, że istotnie tak jest. Dzielimy więc dalej.
ma być również pierwiastkiem otrzymanego wielomianu stopnia 3. Łatwo sprawdzić, że istotnie tak jest. Dzielimy więc dalej.
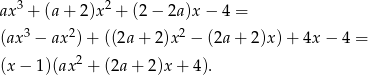
Pozostało sprawdzić, kiedy trójmian w nawiasie jest pełnym kwadratem. Tak jest tylko wtedy gdy 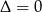 (oba pierwiastki muszą być równe). Mamy więc równanie
(oba pierwiastki muszą być równe). Mamy więc równanie
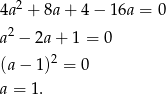
Sposób II
Liczymy podobnie jak poprzednio, ale ponieważ wiemy, że dany wielomian ma się dzielić przez 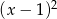 , to dzielimy od razu przez ten wielomian, oszczędzi nam to kroku z wielomianem stonia 3.
, to dzielimy od razu przez ten wielomian, oszczędzi nam to kroku z wielomianem stonia 3.
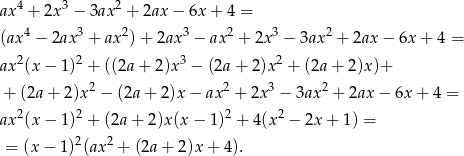
Dalej postępujemy jak poprzednio.
Sposób III
Ponieważ znamy dwa pierwiastki tego wielomianu to wiemy, że musi on być postaci 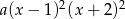 . Wymnażając
. Wymnażając 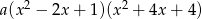 otrzymujemy równanie
otrzymujemy równanie
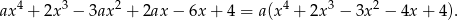
Stąd 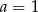 .
.
Sposób IV
Najprostsze rozwiązanie uzyskamy, jeżeli skorzystamy z prostego faktu, że liczba jest pierwiastkiem wielokrotnym wielomianu wtedy i tylko wtedy, gdy jest ona pierwiastkiem pochodnej tego wielomianu. Wiemy zatem, że liczby 1 i -2 muszą być pierwiastkami pochodnej. Liczymy
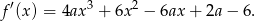
Sprawdzamy teraz, że 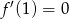 , a
, a 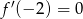 daje
daje 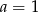 .
.
Odpowiedź: