Zadanie nr 1949340
Wykaż, że jeżeli 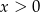 i
i 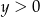 to
to 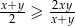 .
.
Rozwiązanie
Sposób I
Przekształcamy nierówność korzystając z podanego założenia.
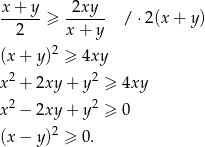
Otrzymana nierówność jest oczywiście prawdziwa, a przekształcaliśmy przy pomocy równoważności, więc wyjściowa nierówność też musi być spełniona.
Sposób II
Tym razem przekształcamy bez mnożenia przez mianownik.
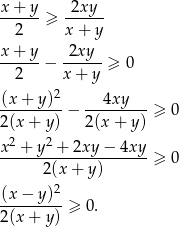
Zarówno licznik jak i mianownik są nieujemne (bo z założenia 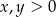 ), zatem nierówność jest spełniona. Przekształcaliśmy w sposób równoważny, więc wyjściowa nierówność też musi być prawdziwa.
), zatem nierówność jest spełniona. Przekształcaliśmy w sposób równoważny, więc wyjściowa nierówność też musi być prawdziwa.

