Zadanie nr 2894561
Niech 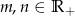 , udowodnij, że jeżeli
, udowodnij, że jeżeli 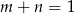 to prawdziwa jest nierówność
to prawdziwa jest nierówność 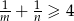 .
.
Rozwiązanie
Sposób I
Korzystamy z nierówności między średnimi: arytmetyczną i harmoniczną
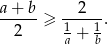
W szczególności, dla 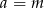 i
i 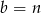 mamy
mamy
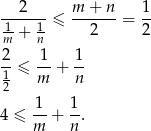
Sposób II
Przekształćmy daną nierówność
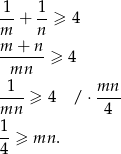
Aby wykazać tę ostatnią nierówność korzystamy z nierówności między średnimi: arytmetyczną i geometryczną
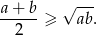
W szczególności dla 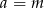 i
i 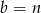 mamy
mamy
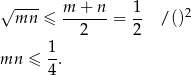
Sposób III
Tak jak poprzednio, przekształcamy nierówność do postaci
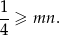
Aby uzasadnić tę nierówność, patrzymy na prawą stronę jak na funkcję zmiennej 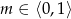 .
.
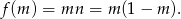
Wykresem tej funkcji jest fragment paraboli o ramionach skierowanych w dół i pierwszej współrzędnej wierzchołka równej 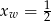 (dokładnie w środku między pierwiastkami).
(dokładnie w środku między pierwiastkami).
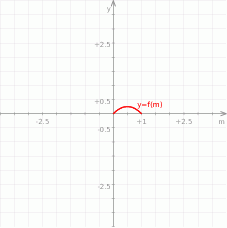
Zatem największą możliwą wartością funkcji 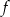 jest
jest
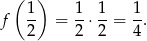
Stąd