Zadanie nr 3799561
Wykaż, że jeżeli 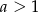 , to
, to 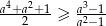 .
.
Rozwiązanie
Przekształcamy równoważnie daną nierówność
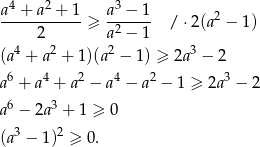
Otrzymana nierówność jest oczywiście spełniona, a przekształcaliśmy przy pomocy równoważności, więc wyjściowa nierówność również musi być prawdziwa.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wykaż, że jeżeli 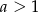 , to
, to 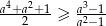 .
.
Przekształcamy równoważnie daną nierówność
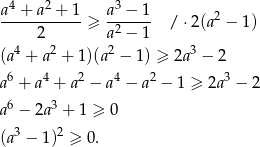
Otrzymana nierówność jest oczywiście spełniona, a przekształcaliśmy przy pomocy równoważności, więc wyjściowa nierówność również musi być prawdziwa.
