/Szkoła średnia/Nierówności/Udowodnij.../Wymierne

Zadanie nr 4133128

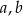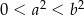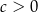Wykaż, że dla każdych trzech liczb a,b i c takich, że 2 2 0 < a < b i c > 0 spełniona jest nierówność

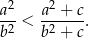
2 2 a--< a-+-c-. b2 b2 + c
Wersja PDF

Rozwiązanie

Przekształcamy nierówność w sposób równoważny – korzystamy przy tym z tego, że każda z liczb: 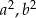a2,b2 i c jest dodatnia.

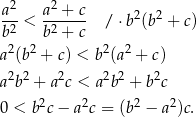
2 2 a--< a--+-c / ⋅b2(b2 + c) b2 b2 + c a2(b 2 + c) < b 2(a 2 + c) a2b 2 + a2c < a 2b2 + b 2c 2 2 2 2 0 < b c− a c = (b − a )c.

Ponieważ z założenia 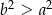2 2 b > a i c > 0 , otrzymana nierówność jest oczywiście prawdziwa. Prawdziwa jest więc też wyjściowa nierówność (bo są one równoważne).

Wersja PDF