/Szkoła średnia/Nierówności/Udowodnij.../Wymierne

Zadanie nr 5075343

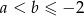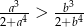Wykaż, że jeżeli a < b ≤ − 2 , to -a3- -b3- 2+a4 > 2+b4 .

Wersja PDF

Rozwiązanie

Aby udowodnić daną nierówność wystarczy wykazać, że funkcja 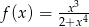-x3- f (x) = 2+x 4 jest malejąca dla 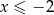x ≤ − 2 . Liczymy pochodną tej funkcji

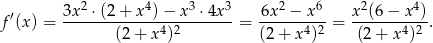
2 4 3 3 2 6 2 4 f ′(x ) = 3x--⋅(2-+-x-)-−-x--⋅4x--= 6x--−-x---= x--(6−--x-). (2 + x4)2 (2+ x4)2 (2 + x4)2

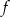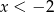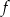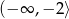Widać teraz, że pochodna funkcji f jest ujemna dla x < − 2 , co oznacza, że f jest malejąca w przedziale (− ∞ ,− 2⟩ .

Wersja PDF