/Szkoła średnia/Nierówności/Udowodnij.../Wymierne

Zadanie nr 6353312

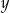Uzasadnij, że dla dowolnych liczb dodatnich x i y prawdziwa jest nierówność

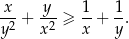
-x-+ y--≥ 1-+ 1. y2 x2 x y
Wersja PDF

Rozwiązanie

Przekształcamy nierówność w sposób równoważny.

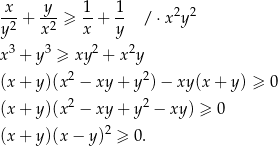
x y 1 1 -2-+ --2 ≥ --+ -- / ⋅x 2y2 y x x y x3 + y3 ≥ xy 2 + x 2y 2 2 (x+ y)(x − xy + y ) − xy (x+ y) ≥ 0 (x+ y)(x2 − xy + y2 − xy ) ≥ 0 (x+ y)(x − y)2 ≥ 0.

Otrzymana nierówność jest oczywiście spełniona (bo 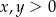x,y > 0 ), więc wyjściowa nierówność też musi być prawdziwa (bo przekształcaliśmy ją w sposób równoważny.

Wersja PDF