Zadanie nr 9348732
Uzasadnij, że dla każdej liczby dodatniej  prawdziwa jest nierówność
prawdziwa jest nierówność 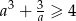 .
.
Rozwiązanie
Sposób I
Przekształcamy nierówność (pamiętamy, że 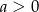 ).
).
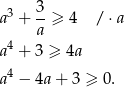
Rozłożymy teraz wielomian z lewej strony nierówności na czynniki.
Łatwo zauważyć, że jednym z pierwiastków jest 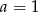 . Dzielimy wielomian przez
. Dzielimy wielomian przez 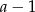 , my zrobimy to grupując wyrazy.
, my zrobimy to grupując wyrazy.
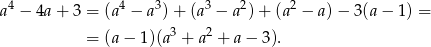
Łatwo zauważyć, że 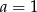 jest pierwiastkiem wielomianu w drugim nawiasie. Dzielimy go przez
jest pierwiastkiem wielomianu w drugim nawiasie. Dzielimy go przez 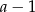 .
.
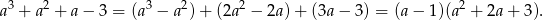
Daną nierówność możemy więc zapisać w postaci
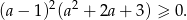
Nierówność ta jest oczywiście spełniona, bo trójmian w drugim nawiasie jest zawsze dodatni (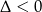 ).
).
Sposób II
Na mocy nierówności
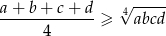
między średnimi: arytmetyczną i geometryczną mamy