/Szkoła średnia/Równania/Liniowe/Rozwiąż równanie

Zadanie nr 2546592

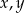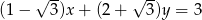Liczby x,y są liczbami naturalnymi, większymi od zera. Określ liczbę rozwiązań równania √ -- √ -- (1 − 3 )x+ (2+ 3)y = 3 .

Wersja PDF

Rozwiązanie

Liczymy

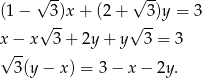
√ -- √ -- (1 − √ 3)x + (2 + √ 3)y = 3 x − x 3 + 2y + y 3 = 3 √ -- 3(y − x ) = 3− x− 2y.

Ponieważ 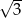√ -- 3 jest liczbą niewymierną, a prawa strona jest zawsze liczbą całkowitą, więc obie strony równania muszą być równe 0.

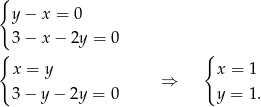
{ y− x = 0 3− x− 2y = 0 { { x = y ⇒ x = 1 3− y− 2y = 0 y = 1.

Zatem równanie ma dokładnie jedno rozwiązanie 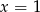x = 1 i y = 1 .  
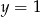Odpowiedź: Istnieje dokładnie jedno rozwiązanie

Wersja PDF