/Szkoła średnia/Zadania z treścią/Geometryczne

Zadanie nr 5926713

Dodaj do ulubionych
Dodaj do rozwiązanych

Z dwóch okrągłych kawałków blachy o średnicy 25 cm wycięto dwa prostokąty w ten sposób, że wierzchołki prostokątów znajdowały się na brzegu kół (patrz rysunek).

PIC

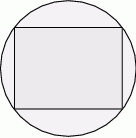
Pierwszy prostokąt miał długość o 4 cm większą niż drugi prostokąt, ale szerokość o 8 cm mniejszą. Oblicz długość i szerokość każdego z prostokątów.

Rozwiązanie

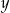Powiedzmy, że pierwszy prostokąt ma długość x i szerokość y . Wtedy drugi prostokąt ma długość 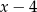x − 4 i szerokość y + 8 .

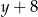Zauważmy teraz, że średnica okręgu to dokładnie długość przekątnej każdego z prostokątów.

PIC

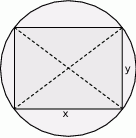
Tak jest, bo środkiem okręgu opisanego na prostokącie jest punkt przecięcia jego przekątnych. Mamy zatem układ równań (twierdzenie Pitagorasa w każdym prostokącie).

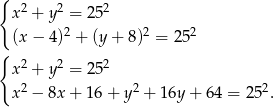
{ x2 + y2 = 252 2 2 2 (x− 4) + (y+ 8) = 25 { 2 2 2 x + y = 25 x2 − 8x + 16 + y2 + 16y + 64 = 252.

Odejmijmy od pierwszego równania drugie (żeby skrócić kwadraty).

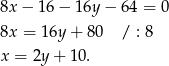
8x − 16− 16y − 64 = 0 8x = 16y + 80 / : 8 x = 2y + 10.

Podstawiamy to wyrażenie do pierwszego równania układu.

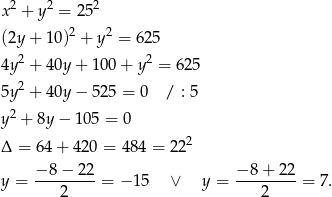
2 2 2 x + y = 25 (2y + 1 0)2 + y 2 = 625 2 2 4y + 4 0y+ 100 + y = 62 5 5y 2 + 4 0y− 525 = 0 / : 5 y 2 + 8y − 1 05 = 0 2 Δ = 64 + 420 = 484 = 2 2 −-8−--22- −-8-+-22- y = 2 = − 1 5 ∨ y = 2 = 7.

Ujemne rozwiązanie odrzucamy i mamy 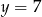y = 7 . Stąd 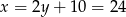x = 2y+ 10 = 24 . Drugi prostokąt ma wymiary: 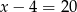x − 4 = 20 i y + 8 = 1 5 .  
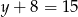Odpowiedź: 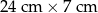24 cm × 7 cm oraz 20 cm × 15 cm

Wersja PDF