Zadanie nr 6021872
Mamy dwa pojemniki: pierwszy ma kształt sześcianu, drugi - ostrosłupa prawidłowego czworokątnego. Przekątna sześcianu ma długość 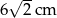 . Wysokość ostrosłupa tworzy ze ścianą boczną kąt o mierze
. Wysokość ostrosłupa tworzy ze ścianą boczną kąt o mierze 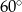 . Pole powierzchni bocznej ostrosłupa jest równe
. Pole powierzchni bocznej ostrosłupa jest równe 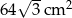 . Sprawdź na podstawie odpowiednich obliczeń, czy woda wypełniająca całkowicie pierwszy pojemnik zmieści się w drugim pojemniku.
. Sprawdź na podstawie odpowiednich obliczeń, czy woda wypełniająca całkowicie pierwszy pojemnik zmieści się w drugim pojemniku.
Rozwiązanie
Obliczmy najpierw objętość sześcianu.
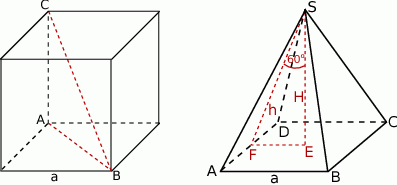
Jeżeli oznaczmy przez  długość krawędzi sześcianu to przekątna w podstawie ma długość
długość krawędzi sześcianu to przekątna w podstawie ma długość 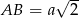 , a przekątna sześcianu
, a przekątna sześcianu
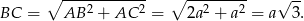
Mamy więc
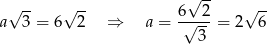
i objętość sześcianu jest równa
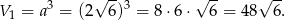
Patrzymy teraz na ostrosłup. Oznaczmy przez  długość jego krawędzi podstawy, przez
długość jego krawędzi podstawy, przez 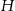 długość jego wysokości, a przez
długość jego wysokości, a przez 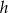 długość wysokości ściany bocznej.
długość wysokości ściany bocznej.
Z trójkąta 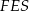 mamy
mamy
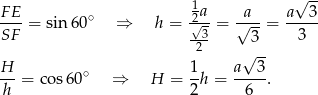
Pole ściany bocznej jest równe 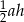 , więc wiemy, że
, więc wiemy, że
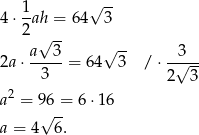
Liczymy objętość ostrosłupa
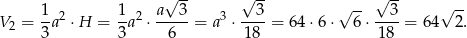
Pozostało sprawdzić, która z liczb 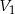 , czy
, czy 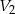 jest większa. Można to zrobić na kalkulatorze, można też zauważyć, że
jest większa. Można to zrobić na kalkulatorze, można też zauważyć, że
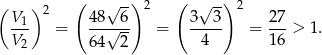
Objętość sześcianu jest więc większa i woda nie zmieści się w drugim pojemniku.
Odpowiedź: Nie, nie zmieści się.

