/Szkoła średnia/Zadania z treścią/Geometryczne

Zadanie nr 6627267

Dodaj do ulubionych
Dodaj do rozwiązanych

W wyniku tzw. złotego podziału odcinka otrzymuje się dwa nowe odcinki o tej własności, że stosunek krótszego z nich do dłuższego jest równy stosunkowi dłuższego z nich do całego odcinka. Dokonano złotego podziału odcinka o długości 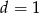d = 1 , oblicz długość krótszej części.

Rozwiązanie

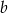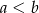Oanaczmy części podziału przez a i b , a < b . Mamy zatem

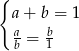
{ a + b = 1 ab = b1

Z drugiego równania mamy 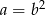a = b2 . Wstawiając do pierwszego dostajemy

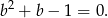
b2 + b − 1 = 0.

Dalej, 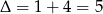Δ = 1 + 4 = 5 i dodatni pierwiastek to 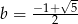√ - b = −-1+--5 2 . Stąd

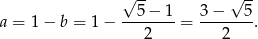
√ -- √ -- 5 − 1 3− 5 a = 1− b = 1− --------= -------. 2 2

 
Odpowiedź: 3−-√5 2

Wersja PDF