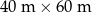/Szkoła średnia/Zadania z treścią/Geometryczne

Zadanie nr 8788209

Dodaj do ulubionych
Dodaj do rozwiązanych

Pole każdej z dwóch prostokątnych działek jest równe 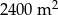2 2 400 m . Szerokość pierwszej działki jest o 8 m większa od szerokości drugiej, ale jej długość jest o 10 m mniejsza. Oblicz szerokość i długość każdej z działek.

Rozwiązanie

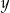Niech x oznacza szerokość pierwszej działki, a y jej długość. W takim razie druga działka ma szerokość 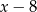x − 8 i długość 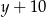y + 10 . Podane pola powierzchni dają układ równań.

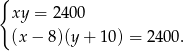
{ xy = 2400 (x − 8)(y + 10) = 2400.

Podstawmy 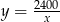2400 y = -x-- z pierwszego równania do drugiego.

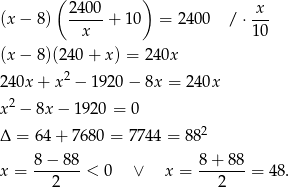
( ) (x − 8) 2400-+ 10 = 2 400 / ⋅ x-- x 10 (x − 8)(24 0+ x ) = 240x 240x + x2 − 1920 − 8x = 240x 2 x − 8x − 19 20 = 0 Δ = 64 + 7680 = 7744 = 8 82 x = 8−--88-< 0 ∨ x = 8-+-88-= 48. 2 2

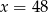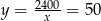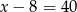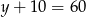Ujemne rozwiązanie odrzucamy i mamy x = 48 . Stąd 2400 y = -x--= 50 . Druga działka ma wymiary x− 8 = 40 i y + 10 = 60 .  
Odpowiedź: 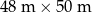48 m × 50 m oraz 40 m × 60 m

Wersja PDF