/Szkoła średnia/Zadania z treścią/Geometryczne

Zadanie nr 9149080

Dodaj do ulubionych
Dodaj do rozwiązanych

Paweł zamówił szybę w kształcie rombu o przekątnych 40 cm i 30 cm. Zaproponował szklarzowi, by wyciął romb z prostokątnego kawałka szyby, tak jak na rysunku. Jakie wymiary ma ten prostokątny kawałek szyby?

PIC

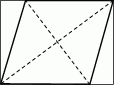
Rozwiązanie

Przyjmijmy oznaczenia z rysunku.

PIC

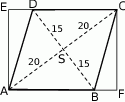
Ponieważ przekątne rombu dzielą się na połowy i są prostopadłe, trójkąt 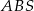ABS jest prostokątny i jego przyprostokątne mają długości 20 i 15. Możemy więc wyliczyć długość boku rombu (korzystamy z twierdzenia Pitagorasa)

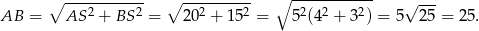
------------ ∘ ---2------2 ∘ ---2-----2 ∘ 2 2 2 √ --- AB = AS + BS = 20 + 15 = 5 (4 + 3 ) = 5 2 5 = 25.

Długości boków prostokąta 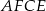AF CE obliczymy na dwa sposoby.

Sposób I

Zauważmy, że odcinek 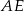AE jest wysokością rombu, więc możemy wyliczyć jego długość ze wzoru na pole rombu. Pole to możemy obliczyć na dwa sposoby

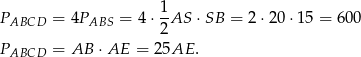
1 PABCD = 4PABS = 4 ⋅-AS ⋅SB = 2 ⋅20 ⋅15 = 60 0 2 PABCD = AB ⋅AE = 25AE .

Mamy zatem równanie

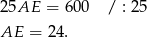
25AE = 600 / : 25 AE = 2 4.

Długość odcinka 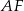AF możemy wyliczyć z twierdzenia Pitagorasa w trójkącie 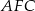AF C . Liczymy

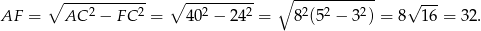
∘ ------------ ∘ ---------- ∘ ------------ √ --- AF = AC 2 − FC 2 = 4 02 − 2 42 = 82(52 − 32) = 8 16 = 32.

Sposób II

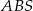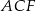Zauważmy, że trójkąty ABS i ACF są prostokątne i mają kąt wspólny 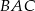BAC . Są więc podobne i mamy

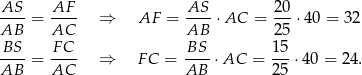
AS AF AS 20 ----= ---- ⇒ AF = ----⋅AC = ---⋅40 = 32 AB AC AB 25 -BS-= F-C- ⇒ FC = -BS-⋅ AC = 1-5⋅ 40 = 24. AB AC AB 2 5

 
Odpowiedź: 24 cm i 32 cm

Wersja PDF