/Szkoła średnia/Zadania z treścią/Geometryczne

Zadanie nr 9382833

Dodaj do ulubionych
Dodaj do rozwiązanych

W dwóch szkołach wybudowano prostokątne baseny. W pierwszej z nich powierzchnia basenu wynosi 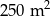25 0 m 2 , w drugiej zaś jest o 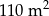110 m 2 większa, a boki prostokąta odpowiednio dłuższe o 2 m na szerokości i o 5 m na długości basenu. Oblicz wymiary basenów w obu szkołach.

Rozwiązanie

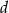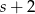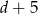Oznaczmy szerokość i długość pierwszego basenu przez s i d . W takim razie drugi basen ma wymiary s+ 2 i d + 5 i otrzymujemy układ równań

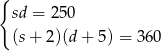
{ sd = 250 (s+ 2)(d + 5 ) = 360

Przekształćmy drugie równanie korzystając z równości 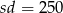sd = 250 .

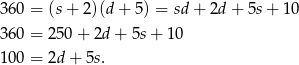
3 60 = (s+ 2)(d + 5) = sd + 2d + 5s + 10 3 60 = 250 + 2d + 5s + 10 1 00 = 2d + 5s.

Podstawiamy teraz do tej równości 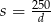250 s = d .

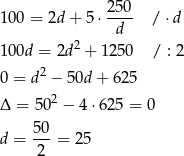
250 10 0 = 2d + 5 ⋅---- / ⋅d d 10 0d = 2d2 + 12 50 / : 2 2 0 = d − 50d + 625 Δ = 502 − 4 ⋅625 = 0 d = 50-= 25 2

Stąd 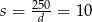250 s = -d- = 10 . Zatem baseny mają wymiary 10 m na 25 m i 12 m na 30 m.  
Odpowiedź: 10 m na 25 m i 12 m na 30 m

Wersja PDF