Zadanie nr 9725335
Z kawałka materiału w kształcie czworokąta wypukłego o obwodzie 8m wycięto koło o polu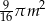 
styczne do wszystkich boków czworokąta. Oblicz pole figury powstałej z tego czworokąta po wycięciu koła, z dokładnością do 
.
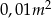Rozwiązanie
Zacznijmy od szkicowego rysunku.
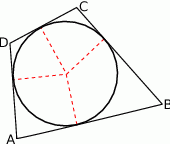
W rozwiązaniu skorzystamy ze wzoru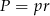 
na pole czworokąta opisanego na okręgu, gdzie 
jest promieniem okręgu wpisanego, a 
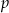jest połową obwodu tego czworokąta. Wzór ten łatwo wyprowadzić dzieląc czworokąt na cztery trójkąty, łącząc wierzchołki tego czworokąta ze środkiem okręgu wpisanego.
Z podanego pola koła wpisanego wiemy, że jego promień jest równy 
. Zatem pole czworokąta jest równe
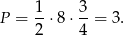
Po wycięciu koła pozostanie nam pole
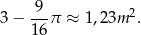
Odpowiedź: 
