/Szkoła średnia/Prawdopodobieństwo/Z definicji/Liczba osób

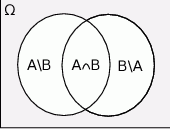
Zadanie nr 2518668

Prawdopodobieństwo tego, że z pewnej grupy osób wylosujemy osobę znającą język angielski jest równe 0,4, prawdopodobieństwo wylosowania osoby znającej język francuski jest równe 0,2, natomiast prawdopodobieństwo wylosowania osoby znającej oba te języki jest równe 0,1. Wykaż, że prawdopodobieństwo wylosowania osoby, która zna język angielski i nie zna języka francuskiego jest trzy razy większe od prawdopodobieństwa wylosowania osoby, która zna język francuski i nie zna języka angielskiego.

Wersja PDF

Rozwiązanie

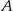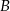Jeżeli oznaczymy przez A i B zdarzenia polegające na wybraniu osoby, która zna odpowiednio język angielski i francuski, to wiemy, że

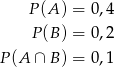
P (A) = 0,4 P (B) = 0,2 P (A ∩ B) = 0,1

To oznacza, że

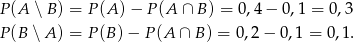
P(A ∖ B ) = P(A )− P(A ∩ B) = 0,4 − 0 ,1 = 0,3 P(B ∖ A ) = P(B )− P(A ∩ B ) = 0,2 − 0,1 = 0 ,1.

Zatem rzeczywiście 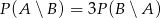P(A ∖ B ) = 3P(B ∖ A ) .

PIC

Wersja PDF