/Szkoła średnia/Prawdopodobieństwo/Z definicji/Liczba osób

Zadanie nr 4072868

Grupa 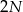2N chłopców i 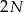2N dziewcząt podzieliła się losowo na 2 równoliczne grupy. Jakie jest prawdopodobieństwo, że w każdej z tych grup jest tyle samo chłopców co dziewcząt?

Wersja PDF

Rozwiązanie

Podział, o którym mowa jest jednoznacznie wyznaczony przez wybór jednej grupy. Jeżeli zatem za zdarzenia elementarne uznamy skład wylosowanej grupy, to

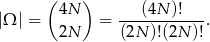
( ) 4N ---(4N-)!--- |Ω | = 2N = (2N )!(2N )!.

Zdarzenia sprzyjające to takie, że w wylosowanej grupie jest tyle samo dziewcząt co chłopców (wtedy w drugiej grupie też tak jest), czyli że w tej grupie jest 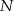N chłopców i 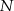N dziewcząt. Takich zdarzeń jest

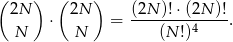
( 2N ) ( 2N ) (2N )!⋅(2N )! ⋅ = ---------4---. N N (N !)

Zatem szukane prawdopodobieństwo wynosi

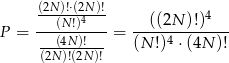
(2N)!⋅(2N)! ---(N!)4--- ((2N )!)4 P = ---(4N-)!-- = -----4------- (2N-)!(2N)! (N !) ⋅(4N )!

 
Odpowiedź: --((2N)!)4-- (N !)4⋅(4N)!

Wersja PDF