/Szkoła średnia/Prawdopodobieństwo/Z definicji/Liczba osób

Zadanie nr 4191388

Dodaj do ulubionych
Dodaj do rozwiązanych

Sześciu pasażerów wsiada do tramwaju złożonego z trzech wagonów. Każdy losowo wybiera wagon. Jakie jest prawdopodobieństwo, że pasażerowie znajdują się w dokładnie dwóch wagonach?

Rozwiązanie

W rozwiązaniu będziemy wykorzystywać zasadę mnożenia. Powiedzmy, że zdarzenia elementarne to ciągi długości 6, których elementami są numery wagonów, do których wsiedli kolejni pasażerowie. Np. ciąg

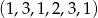
(1,3,1,2 ,3,1)

oznacza, że pierwsza osoba wsiadła do pierwszego wagonu, druga do trzeciego itd.

Mamy zatem

6 |Ω | = 3

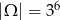
(każdy element ciągu możemy wybrać na 3 sposoby).

Policzmy ilość zdarzeń sprzyjających. Dwa wagony możemy wybrać na

( ) 3 2 = 3

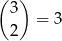
sposoby. Potem każdy pasażer może wybrać jeden z dwóch co daje nam 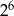26 ciągów. Od tej liczby musimy jednak odjąć dwa ciągi stałe, odpowiadające sytuacji, gdy wszyscy są w jednym wagonie. Zatem prawdopodobieństwo wynosi

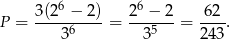
3(26 − 2) 26 − 2 62 P = ----------= -------= ---. 36 35 243

 
Odpowiedź: 62 243

Wersja PDF