Zadanie nr 5001205
Do windy na parterze budynku wsiadło 6 osób, po czym każda z nich w sposób losowy wysiadła na jednym z trzech pięter budynku. Jakie jest prawdopodobieństwo, że na żadnym z pięter nie wysiadły więcej niż 4 osoby?
Rozwiązanie
Za zdarzenia elementarne przyjmijmy ciągi numerów pięter, na których wysiadają kolejne osoby. Zatem
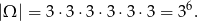
Zamiast zajmować się zdarzeniem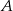 
opisanym w treści zadania, zajmijmy się zdarzeniem przeciwnym 
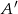tzn. takim, w którym na jednym z pięter wysiadło 6 lub 5 osób.
Są trzy zdarzenia, w których wszystkie osoby wysiadły na jednym piętrze (bo są trzy możliwe wybory piętra).
Obliczmy, ile jest zdarzeń, w których na jednym z pięter wysiada 5 osób. Numer tego piętra możemy wybrać na 3 sposoby, do tego wybieramy 5 osób, które mają na nim wysiąść – możemy to zrobić na
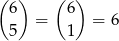
sposobów. To jeszcze nie koniec, bo musimy spośród pozostałych 2 pięter wybrać to, na którym wysiądzie 6-sta osoba. W sumie jest więc
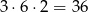
zdarzeń tego typu i prawdopodobieństwo zdarzenia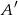 
jest równe
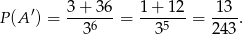
Stąd
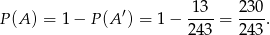
Odpowiedź: 
