Zadanie nr 5774029
W pewnej klasie okazało się, że są 3 osoby, które urodziły się w kwietniu tego samego roku i są dwie osoby, które urodziły się w lipcu tego samego roku. Oblicz prawdopodobieństwo, że troje z tych 5 uczniów urodziło się tego samego dnia roku.
Rozwiązanie
Każdy z uczniów urodzonych w kwietniu mógł urodzić się w jednym z 30 dni kwietnia, a każdy z uczniów urodzonych w lipcu mógł urodzić się w jednym z 31 dni lipca. Zatem wszystkich możliwych dat urodzin jest
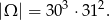
Jeżeli troje z tych uczniów urodziło się tego samego dnia, to musi to być trójka uczniów urodzonych w kwietniu. Mamy zatem
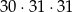
sprzyjających dat urodzin (30 możliwości na wspólny dzień urodzin dla uczniów z kwietnia, a pozostali uczniowie mogą mieć dowolne daty urodzin). Stąd
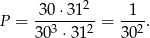
Odpowiedź: