/Szkoła średnia/Prawdopodobieństwo/Z definicji/Liczba osób

Zadanie nr 6298158

Dodaj do ulubionych
Dodaj do rozwiązanych

Na stacji czekało na pociąg 10 pasażerów. Przyjechał pociąg składający się z 7 wagonów. Jakie jest prawdopodobieństwo, że wszyscy pasażerowie wsiedli tylko do dwóch wagonów, jeśli pasażerowie losowo wybierali wagony?

Rozwiązanie

Za zdarzenia elementarne przyjmijmy ciągi z numerami wagonów, do których wsiedli kolejni pasażerowie. Każdy z pasażerów może wybrać jeden z 7 wagonów, co daje nam

|Ω | = 7 10.

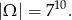
Pozostało policzyć zdarzenia sprzyjające. Dwa wagony z siedmiu możemy wybrać na

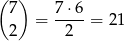
( ) 7 7 ⋅6 = ---- = 2 1 2 2

sposobów. Do tego musimy policzyć na ile sposobów można rozmieścić 10 osób w tych wagonach. Można to zrobić na

10 2

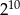
sposobów (każda osoba wybiera jeden z dwóch wagonów). Jest tylko małe ’ale’: trzeba odjąć dwa ustawienia, w których wszyscy wsiadają do tego samego wagonu. W sumie jest więc

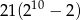
2 1(210 − 2 )

zdarzeń sprzyjających i prawdopodobieństwo wynosi

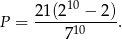
10 P = 2-1(2--−-2-). 710

 
Odpowiedź: 10 21(21−0-2) 7

Wersja PDF