Zadanie nr 6429332
Test na rzadką chorobę, którą dotknięta jest średnio jedna osoba na tysiąc, daje fałszywą pozytywną odpowiedź w 5% przypadków (u osoby chorej daje zawsze odpowiedź pozytywną). Jaka jest szansa, że osoba, u której test dał odpowiedź pozytywną, jest faktycznie chora?
Rozwiązanie
Sposób I
Powiedzmy, że badamy  osób. Spośród nich
osób. Spośród nich 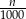 jest chorych. Zatem jest
jest chorych. Zatem jest
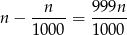
zdrowych i test wykaże wśród nich
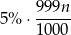
osób chorych. Zatem test daje pozytywną odpowiedź dla
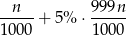
osób. Spośród nich chorych jest 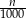 co daje nam prawdopodobieństwo
co daje nam prawdopodobieństwo
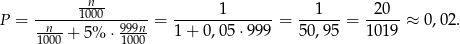
Sposób II
O zadaniu można też myśleć jak o prawdopodobieństwie warunkowym 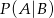 , gdzie
, gdzie 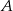 jest zdarzeniem, że osoba jest chora, a
jest zdarzeniem, że osoba jest chora, a 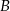 jest zdarzeniem, że test dał pozytywny wynik. Mamy
jest zdarzeniem, że test dał pozytywny wynik. Mamy
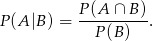
Ponieważ na osobach chorych test jest zawsze pozytywny, mamy
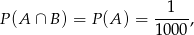
a 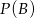 liczymy podobnie jak poprzednio:
liczymy podobnie jak poprzednio:
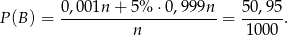
Zatem
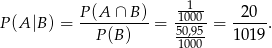
Odpowiedź: