Zadanie nr 8503124
Grupa 4 kobiet i 4 mężczyzn, w tym jedno małżeństwo, wybrała się na pieszą wycieczkę. Na wąskiej ścieżce musieli iść gęsiego tzn. jedno za drugim. Zakładamy, że wszystkie możliwe ustawienia tych osób są jednakowo prawdopodobne. Oblicz prawdopodobieństwo zdarzenia, że jako pierwsze pójdą kobiety i żona będzie szła bezpośrednio przed mężem. Sprawdź, czy to prawdopodobieństwo jest mniejsze od 0,001.
Rozwiązanie
Jak zwykle w zadaniach z prawdopodobieństwa najważniejsze jest odpowiednie ustalenie przestrzeni 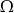 zdarzeń elementarnych. W tym przypadku za
zdarzeń elementarnych. W tym przypadku za 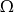 najwygodniej wziąć wszystkie możliwe ustawienia 8 osób. Mamy zatem
najwygodniej wziąć wszystkie możliwe ustawienia 8 osób. Mamy zatem
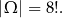
No dobrze, pozostały zdarzenia sprzyjające. Pierwsze mają iść kobiety i ta jedna wyróżniona ma iść na końcu (bo ma iść przed mężem), czyli dla kobiet mamy 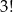 możliwości (kolejność pierwszych trzech). Podobnie dla mężczyzn, mąż musi iść pierwszy, reszta dowolnie, czyli też
możliwości (kolejność pierwszych trzech). Podobnie dla mężczyzn, mąż musi iść pierwszy, reszta dowolnie, czyli też 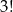 . Zatem zdarzeń sprzyjających jest
. Zatem zdarzeń sprzyjających jest
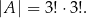
Stąd szukane prawdopodobieństwo wynosi
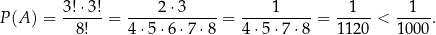
Odpowiedź: