/Szkoła średnia/Prawdopodobieństwo/Z definicji/Liczba osób

Zadanie nr 8768370

Do windy na parterze budynku wsiadło 8 osób, po czym każda z nich w sposób losowy wysiadła na jednym z pięciu pięter budynku. Jakie jest prawdopodobieństwo, że na dwóch różnych piętrach wysiadły po trzy osoby?

Wersja PDF

Rozwiązanie

Za zdarzenia elementarne przyjmijmy ciągi numerów pięter, na których wysiadają kolejne osoby. Zatem

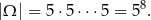
|Ω | = 5 ⋅5⋅⋅⋅ 5 = 58.

Dwa piętra na których mają wysiąść po 3 osoby możemy wybrać na

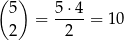
( ) 5 = 5-⋅4 = 1 0 2 2

sposobów. Musimy teraz wybrać 3 osoby, które wysiądą na pierwszym z nich – możemy to zrobić na

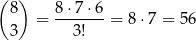
( ) 8 8 ⋅7 ⋅6 3 = ---3!-- = 8 ⋅7 = 5 6

sposobów. Potem wybieramy 3 osoby, które wysiądą na drugim z ustalonych dwóch pięter – możemy to zrobić na

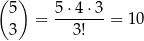
( 5) 5⋅ 4⋅3 = -------= 10 3 3!

sposobów. Na koniec musimy jeszcze wybrać piętra, na których wysiądą pozostałe dwie osoby – możemy to zrobić na

3⋅ 3 = 9

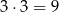
sposobów (każdy z nich może wysiąść na jednym z pozostałych 3 pięter).

Interesujące nas prawdopodobieństwo jest więc równe

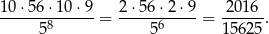
10⋅5-6⋅10-⋅9-= 2-⋅56⋅-2⋅9-= -2016-. 58 56 156 25

 
Odpowiedź: -2016- 15625

Wersja PDF