/Szkoła średnia/Prawdopodobieństwo/Z definicji/Liczba osób

Zadanie nr 8824565

Przedstawiono informacje dotyczące znajomości języka angielskiego oraz języka niemieckiego w pewnej 200 osobowej grupie studentów:
25% studentów zna język angielski i język niemiecki,
50% studentów zna język niemiecki,
60% zna język angielski.
Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że losowo wybrany z tej grupy student

  • zna język angielski i nie zna języka niemieckiego,
  • nie zna języka angielskiego i nie zna języka niemieckiego.
Wersja PDF

Rozwiązanie

Od razu należy pozbyć się tej przerośniętej treści i zamienić ją na literki. Oznaczmy przez 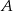A prawdopodobieństwo, że losowy student zna angielski, a 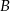B , że zna niemiecki. Mamy dane:

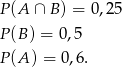
P(A ∩ B ) = 0,25 P(B ) = 0,5 P(A ) = 0,6.
  • Mamy obliczyć P (A ∖ B) .
    PIC

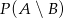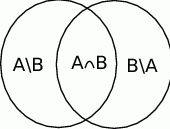
    Jeżeli narysujemy sobie obrazek, to widać, że

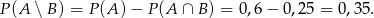
    P(A ∖B ) = P (A) − P (A ∩ B) = 0,6− 0,25 = 0,35 .

     
    Odpowiedź: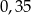 0,35

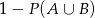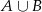  • Mamy obliczyć 1 − P(A ∪ B) (bo A ∪ B to ci którzy znają co najmniej jeden język). Mamy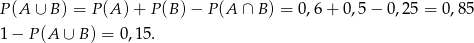
    P (A ∪ B) = P(A )+ P(B )− P (A ∩ B ) = 0,6 + 0,5 − 0,25 = 0,85 1 − P (A ∪ B) = 0,15.

     
    Odpowiedź: 0,15

Wersja PDF