/Szkoła średnia/Prawdopodobieństwo/Z definicji/Liczba osób

Zadanie nr 9538321

W pewnej szkole 47% uczniów uczęszcza na kółko plastyczne, a 65% uczniów uczęszcza na kółko muzyczne. Wiadomo ponadto, że 30% uczniów uczęszcza na obydwa kółka. Oblicz prawdopodobieństwo, że losowy wybrany uczeń tej szkoły nie uczęszcza na żadne z tych kółek.

Wersja PDF

Rozwiązanie

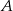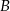Jeżeli oznaczymy przez A i B zdarzenia polegające na wybraniu ucznia, który uczęszcza odpowiednio na kółko plastyczne i muzyczne, to wiemy, że

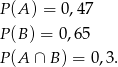
P(A ) = 0,4 7 P(B ) = 0,65 P(A ∩ B) = 0,3 .

W takim razie prawdopodobieństwo wybrania ucznia, który chodzi na jedno z kółek jest równe

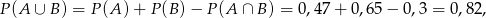
P(A ∪ B) = P (A) + P (B) − P (A ∩ B) = 0,47+ 0,65 − 0,3 = 0,8 2,

a prawdopodobieństwo wybrania ucznia, który nie chodzi na żadne z kółek wynosi

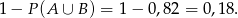
1− P (A ∪ B ) = 1 − 0,82 = 0 ,18.

 
Odpowiedź: 0,18

Wersja PDF