Zadanie nr 9977841
Dziesięć osób rozdzielono na dwie drużyny po 5 osób. Oblicz prawdopodobieństwo, że osoby 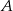 i
i 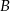 będą w przeciwnych drużynach.
będą w przeciwnych drużynach.
Rozwiązanie
Opisany podział to tak naprawdę wybór 5 osób, które znajdą się w pierwszej drużynie. Za zdarzenia elementarne możemy więc przyjąć (nieuporządkowany) skład pierwszej drużyny. Mamy zatem
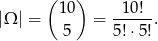
Zastanówmy się ile jest zdarzeń sprzyjających. Jeżeli do pierwszej drużyny wybierzemy osobę 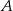 , to trzeba jeszcze dobrać 4 osoby i nie może wśród nich być osoby
, to trzeba jeszcze dobrać 4 osoby i nie może wśród nich być osoby 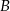 . Takich sytuacji jest zatem.
. Takich sytuacji jest zatem.
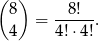
Dokładnie tyle samo jest zdarzeń z osobą 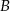 wybraną do pierwszej drużyny.
wybraną do pierwszej drużyny.
Zatem prawdopodobieństwo wynosi
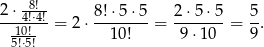
Odpowiedź: