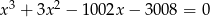/Konkursy/Zadania/Równania/Wielomianowe/Stopnia 3

Zadanie nr 3353470

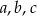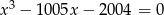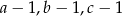Liczby a,b,c są rozwiązaniami równania 3 x − 1005x − 2004 = 0 . Napisz równanie którego rozwiązaniami są liczby a− 1 ,b− 1 ,c− 1 .

Wersja PDF

Rozwiązanie

Sposób I

Jeżeli liczby 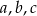a ,b,c są miejscami zerowymi funkcji 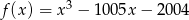f(x) = x3 − 1005x − 20 04 , to liczby 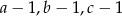a− 1,b− 1,c− 1 będą miejscami zerowymi funkcji, której wykres powstaje z wykresu funkcji 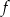f przez przesunięcie o jedną jednostkę w lewo, czyli funkcji

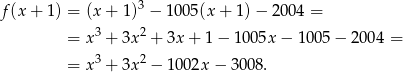
3 f (x+ 1) = (x + 1) − 1005 (x+ 1)− 2004 = = x3 + 3x2 + 3x + 1 − 1 005x − 1005 − 2 004 = 3 2 = x + 3x − 10 02x − 3008.

Sposób II

Wiemy, że

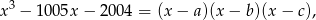
x 3 − 1 005x − 2004 = (x− a)(x − b)(x − c),

a szukane równanie to

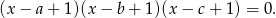
(x − a + 1)(x − b + 1)(x − c + 1) = 0.

Wymnóżmy nawiasy w pierwszej równości.

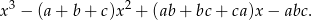
3 2 x − (a+ b+ c)x + (ab + bc + ca)x − abc .

Zatem

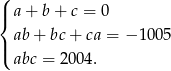
( |{ a + b + c = 0 ab + bc + ca = − 100 5 |( abc = 2 004.

A teraz wymnóżmy nawiasy w docelowym równaniu

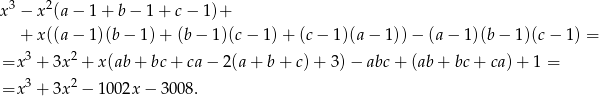
3 2 x − x (a − 1 + b− 1+ c− 1)+ + x((a − 1)(b − 1) + (b− 1)(c− 1)+ (c− 1 )(a − 1 )) − (a − 1)(b − 1)(c − 1) = 3 2 =x + 3x + x(ab + bc + ca − 2(a + b + c) + 3) − abc + (ab + bc+ ca)+ 1 = =x 3 + 3x2 − 100 2x− 3008.

Sposób III

Tak naprawdę, to w poprzednim sposobie wyprowadziliśmy wzory Viéte’a dla równania stopnia 3: jeżeli równanie 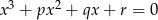3 2 x + px + qx + r = 0 ma trzy pierwiastki to

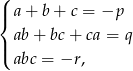
( |{ a+ b+ c = −p ab+ bc+ ca = q |( abc = −r ,

co w naszej sytuacji daje nam

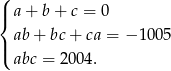
( |{ a + b + c = 0 |( ab + bc + ca = − 100 5 abc = 2 004.

W poszukiwanym równaniu pierwiastkami mają być liczby 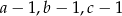a− 1,b− 1,c− 1 , co pozwala nam wyliczyć jego współczynniki

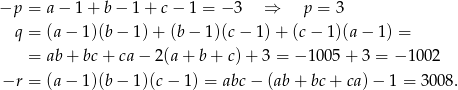
−p = a − 1+ b− 1+ c− 1 = − 3 ⇒ p = 3 q = (a − 1)(b − 1)+ (b− 1)(c− 1)+ (c− 1)(a − 1) = = ab + bc + ca− 2(a+ b+ c)+ 3 = − 1005 + 3 = − 10 02 −r = (a − 1)(b − 1)(c− 1) = abc − (ab + bc + ca) − 1 = 300 8.

Zatem szukane równanie to

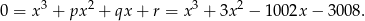
0 = x 3 + px 2 + qx + r = x3 + 3x2 − 100 2x− 3008.

 
Odpowiedź: 3 2 x + 3x − 10 02x − 3008 = 0

Wersja PDF